题目内容
【题目】四边形ABCD中,∠A=145°,∠D=75°.
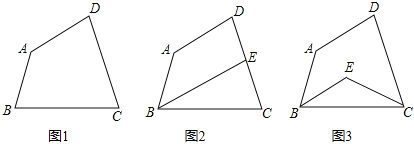
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
【答案】(1)70°;(2)40°;(3)110°.
【解析】
试题分析:(1)根据四边形的内角和即可得到结论;
(2)根据平行线的性质得到∠ABE=35°,∠BED=105°,由∠ABC的角平分线BE交DC于点E,得到∠CBE=∠ABE=35°,根据三角形的外角的性质即可得到结论;
(3)根据四边形的性质得到∠ABC+∠BCD=140°,根据三角形的内角和即可得到结论.
解:(1)∵∠A=145°,∠D=75°,
∴∠B=∠C=![]() (360°﹣145°﹣75°)=70°;
(360°﹣145°﹣75°)=70°;
(2)∵BE∥AD,∠A=145°,∠D=75°,
∴∠ABE=180°﹣∠A=35°,∠BED=180°﹣∠D=105°,
∵∠ABC的角平分线BE交DC于点E,
∴∠CBE=∠ABE=35°,
∴∠C=∠BED﹣∠EBC=40°;
(3)∵∠A=145°,∠D=75°,
∴∠ABC+∠BCD=360°﹣∠A﹣∠C=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=![]() (∠ABC+∠DCB)=70°,
(∠ABC+∠DCB)=70°,
∴∠BEC=110°.

练习册系列答案
相关题目