题目内容
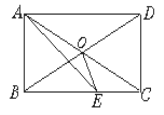
【题目】如图,AD是△ABC的角平分线,将△ABC折叠使点A落在点D处,折痕为EF,则四边形AEDF一定是( )

A. 矩形 B. 菱形 C. 正方形 D. 梯形
【答案】B
【解析】分析:由△ABC折叠使点A落在点D处,折痕为EF,得到∠EAD=∠EDA,∠FAD=∠FDA,根据角平分线的性质推出∠FDA=∠EAD,∠FAD=∠EDA,证出平行四边形AEDF,根据折叠得到AD⊥EF,根据菱形的判定即可得出答案
解答:解:∵将△ABC折叠使点A落在点D处,折痕为EF,
∴∠EAD=∠EDA,∠FAD=∠FDA,
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
∴∠FDA=∠EAD,∠FAD=∠EDA,
∴AE∥DF,DE∥AF,
∴四边形AEDF是平行四边形,
∵将△ABC折叠使点A落在点D处,折痕为EF,
∴∠AOE=∠DOE=90°,
即:AD⊥EF,
∴平行四边形AEDF是菱形.
故选B.

练习册系列答案
相关题目
【题目】为了倡导节约能源,自某日起,我国对居民用电采用阶梯电价,为了使大多数家庭不增加电费支出,事前就需要了解居民全年月平均用电量的分布情况,制订一个合理的方案.某调查人员随机调查了![]() 市
市![]() 户居民全年月平均用电量(单位:千瓦时)数据如下:
户居民全年月平均用电量(单位:千瓦时)数据如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
得到如下频数分布表:
全年月平均用电量/千时 | 频数 | 频率 |
|
|
|
| ||
| ||
|
| |
|
| |
|
| |
合计 |
|
|
画出频数分布直方图,如下:

(1)补全数分布表和率分布直方图
(2)若是根据数分布表制成扇形统计图,则不低于![]() 千瓦时的部分圆心角的度数为_____________;
千瓦时的部分圆心角的度数为_____________;
(3)若![]() 市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗?
市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗?
档次 | 全年月平均用电量/千瓦时 | 电价(元/千瓦时) |
第一档 |
|
|
第二档 |
|
|
第三档 | 大于 |
|