题目内容
(2009•门头沟区一模)已知:如图,在梯形ABCD中,AD∥BC,∠D=90°,∠B=60°,CD= ,BC=9,cos∠DAE=
,BC=9,cos∠DAE= ,求AE的长.
,求AE的长.
【答案】分析:如图,过点A作AF⊥BC于点F,这样把梯形分割成直角三角形和矩形,然后在Rt△AFB中解直角三角形求出BF、AD,最后在Rt△ADE解直角三角形就可以求出AE.
解答: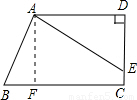 解:如图,过点A作AF⊥BC于点F.(1分)
解:如图,过点A作AF⊥BC于点F.(1分)
∵∠D=90°,
∴AF∥DC.
又∵AD∥BC,
∴四边形AFCD是矩形.
∴FA=CD=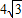 .(2分)
.(2分)
在Rt△AFB中,∠B=60°,
∴BF=AF÷tan60°=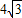 ÷
÷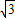 =4.(3分)
=4.(3分)
∴AD=FC=BC-BF=9-4=5.(4分)
在Rt△ADE中,∠D=90°,∵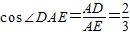 ,
,
∴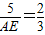 .
.
∴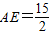 .(5分)
.(5分)
点评:此题考查了梯形的一种常用辅助线-作梯形的高,把梯形分割成直角三角形和矩形,然后解直角三角形就可以解题.
解答:
 解:如图,过点A作AF⊥BC于点F.(1分)
解:如图,过点A作AF⊥BC于点F.(1分)∵∠D=90°,
∴AF∥DC.
又∵AD∥BC,
∴四边形AFCD是矩形.
∴FA=CD=
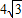 .(2分)
.(2分)在Rt△AFB中,∠B=60°,
∴BF=AF÷tan60°=
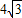 ÷
÷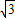 =4.(3分)
=4.(3分)∴AD=FC=BC-BF=9-4=5.(4分)
在Rt△ADE中,∠D=90°,∵
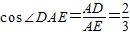 ,
,∴
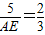 .
.∴
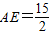 .(5分)
.(5分)点评:此题考查了梯形的一种常用辅助线-作梯形的高,把梯形分割成直角三角形和矩形,然后解直角三角形就可以解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的图象交于A(-2,1)B(1,n)两点.
的图象交于A(-2,1)B(1,n)两点.
 的图象过点A,求反比例函数的解析式.
的图象过点A,求反比例函数的解析式.