题目内容
 如图,从一个直径为4的圆形铁片中剪下一个圆心角为90°的扇形ABC.
如图,从一个直径为4的圆形铁片中剪下一个圆心角为90°的扇形ABC.(1)求这个扇形的面积;
(2)在剩下的材料中,能否从③中剪出一个圆作为底面,与扇形ABC围成一个圆锥?不能,请说明理由;能,请求出剪得圆的半径是多少.
分析:(1)由勾股定理求扇形的半径,再根据扇形面积公式求值.
(2)本题需要求出③中最大圆的直径以及圆锥底面圆的直角(圆锥底面圆的周长即弧BC的长).然后进行比较即可.
(2)本题需要求出③中最大圆的直径以及圆锥底面圆的直角(圆锥底面圆的周长即弧BC的长).然后进行比较即可.
解答: 解:(1)连接BC.
解:(1)连接BC.
由∠BAC=90°得BC为⊙O的直径,
∴BC=4,
在Rt△ABC中,由勾股定理可得:
AB=AC=2
,
∴S扇形ABC=
=2π;
(2)不能.
连接AO并延长交
于点D,交⊙O于点E,则
DE=4-2
.
而l弧BC=
=
π,
设能与扇形围成圆锥体的底面圆的直径为d,
则:dπ=
π,
∴d=
.
又∵DE=4-2
<d=
,即:围成圆锥体的底面圆的直径大于DE,
∴不能围成圆锥体.
 解:(1)连接BC.
解:(1)连接BC.由∠BAC=90°得BC为⊙O的直径,
∴BC=4,
在Rt△ABC中,由勾股定理可得:
AB=AC=2
| 2 |
∴S扇形ABC=
90×π×(2
| ||
| 360 |
(2)不能.
连接AO并延长交
 |
| BC |
DE=4-2
| 2 |
而l弧BC=
90×π×2
| ||
| 180 |
| 2 |
设能与扇形围成圆锥体的底面圆的直径为d,
则:dπ=
| 2 |
∴d=
| 2 |
又∵DE=4-2
| 2 |
| 2 |
∴不能围成圆锥体.
点评:此题主要考查的了圆周角定理、扇形的面积计算方法、弧长公式等知识.关键是熟悉圆锥的展开图和底面圆与圆锥的关系.利用所学的勾股定理、弧长公式及扇形面积公式求值.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
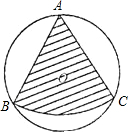 如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为( )
如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
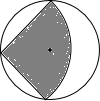 如图,从一个直径为1m的圆形铁片中剪出一个圆心角为90°的扇形,再将剪下的扇形围成一个圆锥,则圆锥的底面半径为
如图,从一个直径为1m的圆形铁片中剪出一个圆心角为90°的扇形,再将剪下的扇形围成一个圆锥,则圆锥的底面半径为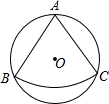 (2012•襄阳)如图,从一个直径为4
(2012•襄阳)如图,从一个直径为4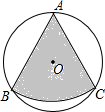 如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为
如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为