题目内容
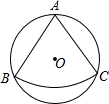（2012•襄阳）如图，从一个直径为4| 3 |
1
1
dm．分析：圆的半径为2
，那么过圆心向AC引垂线，利用相应的三角函数可得AC的一半的长度，进而求得AC的长度，利用弧长公式可求得弧BC的长度，圆锥的底面圆的半径=圆锥的弧长÷2π．
| 3 |
解答：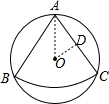
解：作OD⊥AC于点D，连接OA，
∴∠OAD=30°，AC=2AD，
∴AC=2（OA×cos30°）=6
∴
=2π
∴圆锥的底面圆的半径=2π÷（2π）=1．
故答案为：1．
解：作OD⊥AC于点D，连接OA，∴∠OAD=30°，AC=2AD，
∴AC=2（OA×cos30°）=6
∴
| 60π×6 |
| 180 |
∴圆锥的底面圆的半径=2π÷（2π）=1．
故答案为：1．
点评：考查圆锥的计算；用的知识点为：圆锥的侧面展开图弧长等于圆锥的底面周长；难点是得到扇形的半径．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
（2012•襄阳）如图，在△ABC中，AB=AC，AD⊥BC于点D，将△ADC绕点A顺时针旋转，使AC与AB重合，点D落在点E处，AE的延长线交CB的延长线于点M，EB的延长线交AD的延长线于点N．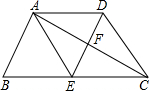
（2012•襄阳）如图，在梯形ABCD中，AD∥BC，E为BC的中点，BC=2AD，EA=ED=2，AC与ED相交于点F．
（2012•襄阳）如图，ABCD是正方形，G是BC上（除端点外）的任意一点，DE⊥AG于点E，BF∥DE，交AG于点F．下列结论不一定成立的是（ ）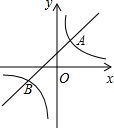
（2012•襄阳）如图，直线y=k1x+b与双曲线y=