题目内容
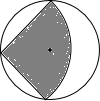 如图,从一个直径为1m的圆形铁片中剪出一个圆心角为90°的扇形,再将剪下的扇形围成一个圆锥,则圆锥的底面半径为
如图,从一个直径为1m的圆形铁片中剪出一个圆心角为90°的扇形,再将剪下的扇形围成一个圆锥,则圆锥的底面半径为分析:利用勾股定理易得扇形的半径,那么就能求得扇形的弧长,除以2π即为圆锥的底面半径.
解答:解:易得扇形的圆心角所对的弦是直径,
∴扇形的半径为:
m,
∴扇形的弧长为:
=
πm,
∴圆锥的底面半径为:
π÷2π=
m.
∴扇形的半径为:
| ||
| 2 |
∴扇形的弧长为:
90π×
| ||||
| 180 |
| ||
| 4 |
∴圆锥的底面半径为:
| ||
| 4 |
| ||
| 8 |
点评:本题用到的知识点为:90度的圆周角所对的弦是直径;圆锥的侧面展开图的弧长等于圆锥的底面周长.

练习册系列答案
相关题目
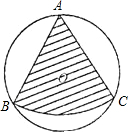 如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为( )
如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
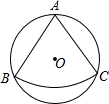 (2012•襄阳)如图,从一个直径为4
(2012•襄阳)如图,从一个直径为4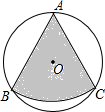 如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为
如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为 如图,从一个直径为4的圆形铁片中剪下一个圆心角为90°的扇形ABC.
如图,从一个直径为4的圆形铁片中剪下一个圆心角为90°的扇形ABC.