题目内容
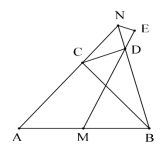
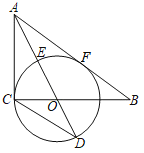
【题目】如图,在Rt△ABC中,∠ACB=90°,O是线段BC上一点,以O为圆心,OC为半径作⊙O,AB与⊙O相切于点F,直线AO交⊙O于点E,D.
(1)求证:AO是△ABC的角平分线;
(2)若tan∠D=![]() ,求
,求![]() 的值;
的值;
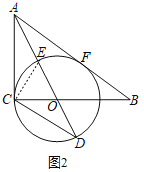
(3)如图2,在(2)条件下,连接CF交AD于点G,⊙O的半径为3,求CF的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)连接OF,可得OF⊥AB,由∠ACB=90°,OC=OF,可得出结论;
(2)连接CE,先求证∠ACE=∠ODC,然后可知△ACE∽△ADC,所以![]() ,结合tan∠D=
,结合tan∠D=![]() =
=![]() ,即可得到结论;
,即可得到结论;
(3)连接CF交AD于点M,由(2)可知,AC2=AEAD,先求出AE,AC的长,则AO可求出,证△CMO∽△ACO,可得OC2=OMOA,求出OM,CM,结合CF=2CM,即可求解.
(1)如图1,连接OF,
∵AB与⊙O相切于点F,
∴OF⊥AB,
∵∠ACB=90°,OC=OF,
∴AO是△ABC的角平分线;
(2)如图2,连接CE,
∵ED是⊙O的直径,
∴∠ECD=90°,
∴∠ECO+∠OCD=90°,
∵∠ACB=90°,
∴∠ACE+∠ECO=90°,
∴∠ACE=∠OCD,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ACE=∠ODC,
∵∠CAE=∠CAE,
∴△ACE∽△ADC,
∴![]() ,
,
∵tan∠D=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ;
;
(3)由(2)可知:![]() =
=![]() ,
,
∴设AE=x,AC=2x,
∵△ACE∽△ADC,
∴![]() ,
,
∴AC2=AEAD,
∴(2x)2=x(x+6),
解得:x=2或x=0(不合题意,舍去),
∴AE=2
∴AO=AE+OE=2+3=5,
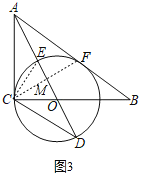
如图3,连接CF交AD于点M,
∵AC,AF是⊙O的切线,
∴AC=AF,∠CAO=∠OAF,
∴CF⊥AO,
∴∠ACO=∠CMO=90°,
∵∠COM=∠AOC,
∴△CMO∽△ACO,
∴![]() ,
,
∴OC2=OMOA,
∴OM=![]() ,
,
∴CM=![]() ,
,
∴CF=2CM=![]() .
.


 名校课堂系列答案
名校课堂系列答案