题目内容
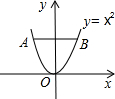 如图,A、B分别为y=x2上两点,且线段AB⊥y轴,若AB=6,则直线AB的表达式为
如图,A、B分别为y=x2上两点,且线段AB⊥y轴,若AB=6,则直线AB的表达式为
- A.y=3
- B.y=6
- C.y=9
- D.y=36
C
分析:根据抛物线的对称性可知B点的横坐标为3,代入抛物线解析式可求B点的纵坐标,从而可得直线AB的表达式.
解答:∵线段AB⊥y轴,且AB=6,
∴由抛物线的对称性可知,B点横坐标为3,
当x=3时,y=x2=32=9,
∴直线AB的表达式y=9.
故选C.
点评:本题考查了抛物线的对称性与点的坐标的关系,关键是根据对称性求B点的横坐标.
分析:根据抛物线的对称性可知B点的横坐标为3,代入抛物线解析式可求B点的纵坐标,从而可得直线AB的表达式.
解答:∵线段AB⊥y轴,且AB=6,
∴由抛物线的对称性可知,B点横坐标为3,
当x=3时,y=x2=32=9,
∴直线AB的表达式y=9.
故选C.
点评:本题考查了抛物线的对称性与点的坐标的关系,关键是根据对称性求B点的横坐标.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
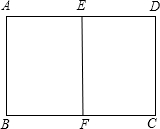 如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD
如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD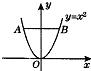 5、如图,A、B分别为y=x2上两点,且线段AB⊥y轴,若AB=6,则直线AB的表达式为( )
5、如图,A、B分别为y=x2上两点,且线段AB⊥y轴,若AB=6,则直线AB的表达式为( )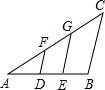 如图,D,E分别为AB的三等分点,DF∥EG∥BC,若BC=12,则DF=
如图,D,E分别为AB的三等分点,DF∥EG∥BC,若BC=12,则DF= 如图,D、E分别为⊙O半径OA、OB的中点,C是
如图,D、E分别为⊙O半径OA、OB的中点,C是
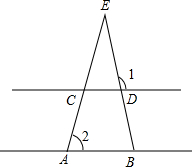 (2012•朝阳)如图,C、D分别为EA、EB的中点,∠E=30°,∠1=110°,则∠2的度数为( )
(2012•朝阳)如图,C、D分别为EA、EB的中点,∠E=30°,∠1=110°,则∠2的度数为( )