题目内容
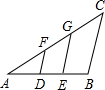如图，D，E分别为AB的三等分点，DF∥EG∥BC，若BC=12，则DF=分析：由于DF∥EG∥BC，可得出△ADF∽△AEG∽△ABC；已知了D、E是AB的三等分点，可得出AD、AE、AB的比例关系，即三个相似三角形的相似比．已知了BC的长，根据三个三角形的相似比即可求出DF和EG的长．
解答：解：∵DF∥EG∥BC
∴△ADF∽△AEG∽△ABC
∴DF：BC=AD：AB，EG：BC=AE：AB
∵D，E分别为AB的三等分点，且BC=12
∴
=
，
=
∴DF=4，EG=8．
∴△ADF∽△AEG∽△ABC
∴DF：BC=AD：AB，EG：BC=AE：AB
∵D，E分别为AB的三等分点，且BC=12
∴
| DF |
| 12 |
| 1 |
| 3 |
| EG |
| 12 |
| 2 |
| 3 |
∴DF=4，EG=8．
点评：本题考查了相似三角形的判定与性质．
相似三角形的对应角相等，对应边的比相等；
三角形一边的平行线交另两边或另两边的延长线组成的三角形与原三角形相似．
相似三角形的对应角相等，对应边的比相等；
三角形一边的平行线交另两边或另两边的延长线组成的三角形与原三角形相似．
练习册系列答案
相关题目
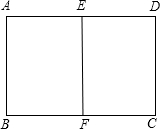如图，E，F分别为矩形ABCD的边AD，BC的中点，若矩形ABCD∽矩形EABF，AB=1．求矩形ABCD
5、如图，A、B分别为y=x2上两点，且线段AB⊥y轴，若AB=6，则直线AB的表达式为（ ）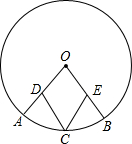
如图，D、E分别为⊙O半径OA、OB的中点，C是
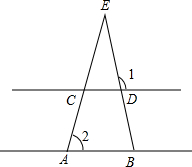（2012•朝阳）如图，C、D分别为EA、EB的中点，∠E=30°，∠1=110°，则∠2的度数为（ ）