题目内容
【题目】在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,与抛物线交于另一点
,与抛物线交于另一点![]() .已知
.已知![]() ,
,![]() .
.
(1)求抛物线与直线的解析式;
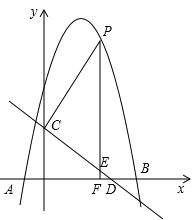
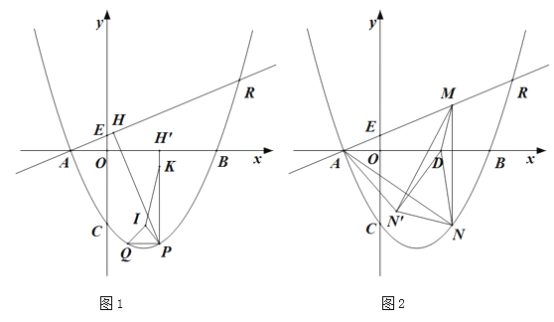
(2)如图1,若点![]() 是
是![]() 轴下方抛物线上一点,过点
轴下方抛物线上一点,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 为直线
为直线![]() 上一点,且
上一点,且![]() .点
.点![]() 为第四象限内一点,且在直线
为第四象限内一点,且在直线![]() 上方,连接
上方,连接![]() 、
、![]() 、
、![]() .记
.记![]() ,
,![]() .当
.当![]() 取得最大值时,求出点
取得最大值时,求出点![]() 的坐标,并求出此时
的坐标,并求出此时![]() 的最小值.
的最小值.
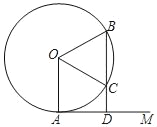
(3)如图2,将点![]() 沿直线
沿直线![]() 方向平移13个长度单位到点
方向平移13个长度单位到点![]() ,过点
,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() .动点
.动点![]() 为
为![]() 轴上一点,连接
轴上一点,连接![]() 、
、![]() ,再将
,再将![]() 沿直线
沿直线![]() 翻折为
翻折为![]() (点
(点![]() 、
、![]() 、
、![]() 、
、![]() 在同一平面内),连接
在同一平面内),连接![]() 、
、![]() 、
、![]() ,当
,当![]() 为等腰三角形时,请直接写出点
为等腰三角形时,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)抛物线:![]() 直线:
直线:![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)求出点A,B,C的坐标,根据待定系数法即可求出抛物线与直线的解析式;
(2)设点![]() ,对称轴为:
,对称轴为:![]() ,根据相似三角形的判定方法得到
,根据相似三角形的判定方法得到![]() 与
与![]() 相似,根据相似三角形的性质得到
相似,根据相似三角形的性质得到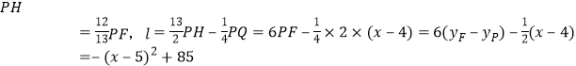 ,根据二次函数的性质即可求出
,根据二次函数的性质即可求出![]() 取得最大值时,求出点
取得最大值时,求出点![]() 的坐标,并求出此时
的坐标,并求出此时![]() 的最小值.
的最小值.
(3)分三种情况进行讨论即可.
(1)令![]()
![]()
![]() .
.
又![]()
把点A、B分别代入![]() 中,得
中,得
![]() 解得:
解得: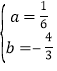
把点A代入直线![]() 中,得
中,得
![]() ,
,
![]() 抛物线的解析式为:
抛物线的解析式为:![]() ,
,
直线的解析式为:![]()
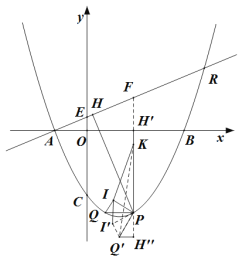
(2)设点![]() ,对称轴为:
,对称轴为:![]() ,由题意,当点
,由题意,当点![]() 在对称轴左侧时的
在对称轴左侧时的![]() 值一定小于点
值一定小于点![]() 在对称轴右侧时的
在对称轴右侧时的![]() 值,所以
值,所以![]() .
.
令![]()
作![]() 轴交直线
轴交直线![]() 与点
与点![]() ,则
,则![]() 与
与![]() 相似。
相似。
所以![]()
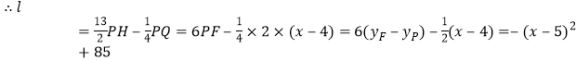
![]() 当
当![]() 时,
时,![]() .此时,点
.此时,点![]() .
.
此时点![]() ,
,![]() .
.
把![]() 绕点
绕点![]() 逆时针旋转60度,得
逆时针旋转60度,得![]() .
.
此时![]()
当点![]() 、
、![]() 、
、![]() 、
、![]() 共线时,
共线时,![]() 取最小值
取最小值![]() .
.
作![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
![]() 的最小值为
的最小值为![]()
(3)![]()

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目