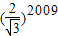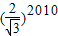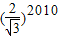题目内容
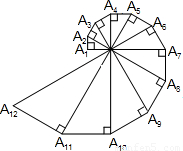
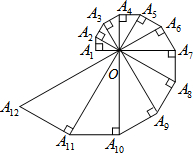 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则A2A3=
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则A2A3=| 4 |
| 3 |
| 4 |
| 3 |
(
)2009
| 2 | ||
|
(
)2009
.| 2 | ||
|
分析:在直角三角形OA1A2中,利用30°所对的直角边等于斜边的一半得到OA2=2A1A2,由A1A2的长求出OA2的长,在直角三角形OA2A3中,利用锐角三角函数定义得到tan∠A2OA3等于A2A3与OA2的比值,求出A2A3的长,再利用30°所对的直角边等于斜边的一半求出OA3的长,同理求出A3A4的长,以此类推得到直角三角形△A2010OA2011的最小边长A2010A2011即可.
解答:解:在Rt△OA1A2中,A1A2=1,∠OA1A2=90°,∠A1OA2=30°,
∴OA2=2A1A2=2,
在Rt△OA2A3中,OA2=2,∠OA2A3=90°,∠A2OA3=30°,
∴A2A3=OA2tan∠A2OA3=2×
=
,OA3=2A2A3=
,
在Rt△OA3A4中,OA3=
,∠OA3A4=90°,∠A3OA4=30°,
∴A3A4=OA3tan∠A3OA4=
×
=
=(
)2,
以此类推,Rt△A2010OA2011的最小边长A2010A2011=(
)2009.
故答案为:
,(
)2009.
∴OA2=2A1A2=2,
在Rt△OA2A3中,OA2=2,∠OA2A3=90°,∠A2OA3=30°,
∴A2A3=OA2tan∠A2OA3=2×
| ||
| 3 |
| 2 | ||
|
| 4 | ||
|
在Rt△OA3A4中,OA3=
| 4 | ||
|
∴A3A4=OA3tan∠A3OA4=
| 4 | ||
|
| ||
| 3 |
| 4 |
| 3 |
| 2 | ||
|
以此类推,Rt△A2010OA2011的最小边长A2010A2011=(
| 2 | ||
|
故答案为:
| 4 |
| 3 |
| 2 | ||
|
点评:此题考查了勾股定理以及含30°角的直角三角形的性质,锐角三角函数定义,属于规律型试题,利用了转化的思想,锻炼了学生归纳总结的能力.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
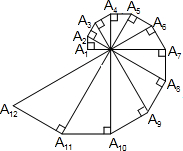 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2010OA2011的最小边长为( )
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2010OA2011的最小边长为( )| A、22009 | ||||
| B、22010 | ||||
C、(
| ||||
D、(
|
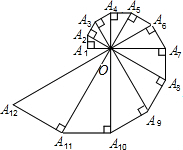 (2012•柳州一模)如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2011OA2012的最小边长为( )
(2012•柳州一模)如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2011OA2012的最小边长为( )