题目内容
【题目】阅读下列两则材料,回答问题,材料一:定义直线y=ax+b与直线y=bx+a互为“共同体直线”,例如,直线y=x+4与直线y=4x+l互为“共同体直线”.
材料二:对于半面直角坐标系中的任意两点P1(x1,y1)、P2(x2,y2),P1、P2之两点间的直角距离d1(P1,p2)=|x1﹣x2|+|y1﹣y2|:例如:Q1(﹣3,1)、Q2(2.4)两点间的直角距离为d(Q1,Q2)=|﹣3﹣2|+|1﹣4|=8; P0(x0,y0)为一个定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做Po到直线y=ax+b的直角距离.
(1)计算S(﹣2,6),T(1,3)两点间的直角距离d(S,T)= ,直线y=4x+3上的一点H(a,b)又是它的“共同体直线”上的点,求点H的坐标.
(2)对于直线y=ax+b上的任意一点M(m,n),都有点N(3m,2m﹣3n)在它的“共同体直线”上,试求点L(10,﹣![]() )到直线y=ax+b的直角距离.
)到直线y=ax+b的直角距离.
【答案】(1)d(S,T)=7,H(1,7);(2)10.
【解析】
(1)根据题中所给出的两点的直角距离公式即可得出结论;求两条直线的交点即可求H点的坐标;
(2)先表示直线y=ax+b的“共同体直线”,并将点M和N分别代入可得方程组,得:(3b+3a﹣2)m=﹣a﹣3b,对于任意一点M(m,n)等式均成立,求出a,b的值,再根据题意得出关于x的式子,再由绝对值的几何意义即可得出结论.
解:(1)∵S(﹣2,6)、T(1,3)则S、T两点的直角距离为d(S,T)=|﹣2﹣1|+|6﹣3|=7,
∴S(﹣2,6)、T(1,3)两点间的直角距离d(S,T)=7.
直线y=4x+3的“共同体直线”是y=3x+4,由题意知H是它们的交点,则有:![]() ,
,
解得![]() ,
,
∴点H的坐标为:H(1,7);
(2)∵点M(m,n)是直线y=ax+b上的任意一点,
∴am+b=n①,
∵点N(3m,2m﹣3n)是直线y=ax+b的“共同体直线”上的一点,
即N(3m,2m﹣3n)在直线y=bx+a上
∴3bm+a=2m﹣3n②,
将①代入②得,3bm+a=2m﹣3(am+b),
整理得:3bm+3am﹣2m=﹣a﹣3b,
∴(3b+3a﹣2)m=﹣a﹣3b,
∵对于任意一点M(m,n)等式均成立,
∴![]() ,
,
解得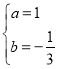 ,
,
![]() .
.
![]() 是直线
是直线![]() 上的动点,定点
上的动点,定点![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() 当
当![]() 时,代数式
时,代数式![]() 有最小值10,
有最小值10,
![]() 点
点![]() 到直线
到直线![]() 的直角距离是10.
的直角距离是10.

 金钥匙试卷系列答案
金钥匙试卷系列答案【题目】随着“西成高铁”的开通,对于加强关中一天水经济区与成渝经济区的交流合作,促进区域经济发展和提高人民出行质量,具有十分重要的意义.成都某单位组织优秀员工利用周末乘坐“西成高铁”到西安观光旅游,计划游览着名景点“大唐芙蓉园”.已知该景区团体票价格设置如下:
人数/人 | 10人以内(含10人) | 超过10人但不超过30人的部分 | 超过30人的部分 |
单价(元/张) | 120 | 100 | 90 |
(1)求团体票总费用y(元)与游览人数x(人)之间的关系式;
(2)若该单位购买团体票共花费4100元,且所有人都购买了门票,那么该单位共有多少人游览了“大唐芙蓉园”?