题目内容
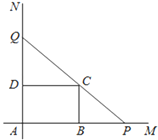
【题目】如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,其中AB=30米,AD=20米.现欲将其扩建成一个三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ经过点C.
(1)DQ=10米时,求△APQ的面积.
(2)当DQ的长为多少米时,△APQ的面积为1600平方米.
【答案】(1)S△APQ =1350米2;(2)DQ的长应设计为60或![]() 米.
米.
【解析】
(1)根据平行线分线段成比例求出AP长即可解题,
(2)根据![]() =
=![]() ,求出AP得长,列出方程即可求解.
,求出AP得长,列出方程即可求解.
(1)∵DC∥AP,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AP=90,
∴S△APQ=![]() AQAP=1350米2;
AQAP=1350米2;
(2)设DQ=x米,则AQ=x+20,
∵DC∥AP,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AP= ![]() ,
,
由题意得 ![]() ×
×![]() ×(x+20)=1600,
×(x+20)=1600,
化简得3x2﹣200 x+1200=0,
解x=60或![]() .
.
经检验:x=60或![]() 是原方程的根,
是原方程的根,
∴DQ的长应设计为60或![]() 米.
米.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目