题目内容
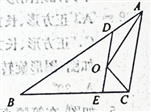
【题目】如图，在△ABC中，AB=5cm，BC=3cm，∠BAC与∠BCA的平分线相交于点O，点D在AB上，且AD=OD，DO的延长线交BC于点E.试求△BDE的周长.
【答案】8cm
【解析】试题分析：根据等腰三角形的性质和角平分线的定义易证∠DOA=∠OAC，即可得DE∥AC，再由角平分线的定义和平行线的性质证得∠EOC=∠ECO，根据等腰三角形的性质可得OE=CE，再由BE+DE+BD=BE+OE+OD+BD=BE+EC+BD+DA=AB+BC即可得△BDE的周长.
试题解析：
∵AD=OD，
∴∠DAO=∠DOA，
∵∠DAO=∠OAC，
∴∠DOA=∠OAC，
∴DE∥AC，
∴∠EOC=∠OCA，
∵∠OCA=∠OCE，
∴∠EOC=∠ECO，
∴OE=CE，
∴BE+DE+BD=BE+OE+OD+BD=BE+EC+BD+DA=AB+BC=5+3=8（cm），
∴△BDE的周长=8cm．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
