题目内容
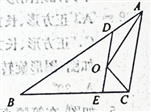
【题目】如图，在平面直角坐标系中，直线AB与x轴，y轴交于点A(10，0)，B(0，－10)，直线MT垂直于直线AB，垂足为M，与y轴交于点T(0，－2) ．
（1）求点M的坐标；
（2）在线段MT的延长线上找一点N，使MT＝TN，求点N的坐标；
（3）若点D在x轴上，∠ABD＝60°，E点在线段BD上运动，∠AEB的平分线交AB于点P，∠EAB的平分线交线段BD于点Q，AQ与EP交于点R． 
的值是多少？
【答案】（1）M(4，－6)（2）N(－4，2)（3）1
【解析】试题分析：（1）M点可以看作是直线AB与直线MN的交点，要求交点坐标即要求出这两条直线的解析式，已知A、B的坐标可以求出直线AB的解析式，结合特殊角可以求出OC的长度，从而求出C的坐标，根据C、T的坐标可以求出直线MN的解析式；（2）作MG⊥y轴于点G，NH⊥y轴于点H，结合已知条件不难证明△NHT≌△MGT，进而求出NH、HO的长度，表示出N的坐标即可；（3）在AE上取一点G，使EQ＝EG ，不难证明△ERG≌△ERQ，由此可得∠EGR=∠ERQ，再由∠AEB的平分线交AB于点P，∠EAB的平分线交线段BD于点Q，∠ABD＝60°可以计算得出∠ERA=120°，进而可以得出∠ERQ=60°，所以∠GRA=∠PRA=60°，接下去不难证明△ARG≌△ARP，可以得出AP=AG，所以
=
=1.
试题解析：
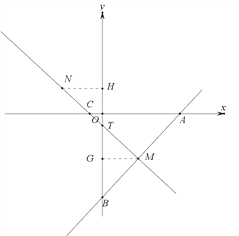
（1）∵A(10，0)，B(0，－10)，
∴AO=BO=10，
∴∠OBA=45°，
∵MN⊥AB，
∴∠TMB=90°，
∴∠BTM=∠CTO=45°，
∴CO=TO，
∵T(0，－2)，
∴CO=TO=2，
∴C（－2，0），
设y=k1x+b1，
，
∴
，
∴y=－x－2，
设直线AB解析式为y2=k2x+b2，
，
∴
，
∴y=x－10，
，
解得
，
∴M（4，－6）；
（2）作MG⊥y轴于点G，NH⊥y轴于点H，
∴∠NHT=∠MGT=90°，
∵在△NHT和△MGT中，
，
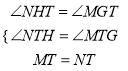∴△NHT≌△MGT，
∴NH=MG=4，HT=GT=4，
∴HO=2，
∴N（－4，2）；
（3）
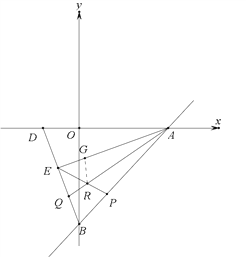
在AE上取一点G，使EQ＝EG ，
∵PE平分∠AEB，QA平分∠EAB，
∴∠AER=
∠AEB，∠EAR=
∠EAB，
∴∠AER+∠EAR =
（∠AEB+∠EAB），
∵∠ABD=60°，
∴∠AEB+∠EAB=120°，
∴∠AER+∠EAR=60°，
∴∠ERA=120°，
∴∠ERQ=60°，
∵PE平分∠AEB，
∴∠GER=∠QER，
∵在△GER和△QER中，
，
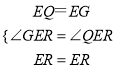∴△GER≌△QER，
∴∠ERG=∠ERQ=60°，
∴∠ARG=60°，∠ARP=60°，
∵在△ARG和△ARP中，
，
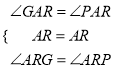∴△ARG≌△ARP，
∴AP=AG，
∴
=
=1.
