Question

【题目】如图，∠MON=60°，作边长为1的正六边形A1B1C1D1E1F1 ， 边A1B1、F1E1分别在射线OM、ON上，边C1D1所在的直线分别交OM、ON于点A2、F2 ， 以A2F2为边作正六边形A2B2C2D2E2F2 ， 边C2D2所在的直线分别交OM、ON于点A3、F3 ， 再以A3F3为边作正六边形A3B3C3D3E3F3 ， …，依此规律，经第4次作图后，点B4到ON的距离是 ．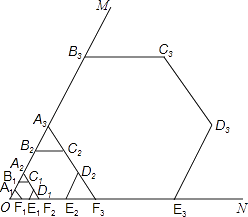

Answer 1

【答案】
【解析】解：观察图象可知OB1=2=2×30，

OB2=2×31，

OB3=2×32=18，

OB4=2×33=54，

∴B4到ON的距离为54sin60°=27 ，

故答案为：

先计算出OB1、OB2、OB3的长，然后依据规律可得到OB4的长，从而可得到B4到ON的距离.