题目内容
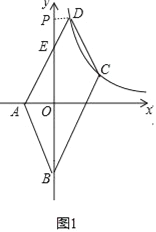
【题目】如图1,已知点A(﹣1,0),点B(0,﹣2),AD与y轴交于点E,且E为AD的中点,双曲线y=![]() 经过C,D两点且D(a,4)、C(2,b).
经过C,D两点且D(a,4)、C(2,b).
(1)求a、b、k的值;
(2)如图2,线段CD能通过旋转一定角度后点C、D的对应点C′、D′还能落在y=![]() 的图象上吗?如果能,写出你是如何旋转的,如果不能,请说明理由;
的图象上吗?如果能,写出你是如何旋转的,如果不能,请说明理由;
(3)如图3,点P在双曲线y=![]() 上,点Q在y轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试求满足要求的所有点P、Q的坐标.
上,点Q在y轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试求满足要求的所有点P、Q的坐标.
【答案】(1)a=1,k=4,b=2 (2)能 (3)P1(1,4),Q1(0,6);P2(﹣1,﹣4),Q2(0,﹣6);P3(﹣1,﹣4),Q3(0,2).
【解析】(1)如图1,过点D做DP⊥y轴于点P,由△PDE≌△OAE(ASA),PD=OA,求出点D坐标,即可解决问题;
(2)能,点C、D绕点O顺时针旋转180度时,点C′、D′落在y=![]() 图象上.或点C、D关于原点中心对称的点在图象上;
图象上.或点C、D关于原点中心对称的点在图象上;
(3)分两种情形分别求解①当AB为边时,如图1中,若四边形ABPQ为平行四边形,则![]() =0;如图2中,若四边形ABQP是平行四边形时,AP=BQ,且AP∥BQ,求点P坐标,即可解决问题;②如图3中,当AB为对角线时,AP=BQ,AP∥BQ,求出点P坐标,即可解决问题.
=0;如图2中,若四边形ABQP是平行四边形时,AP=BQ,且AP∥BQ,求点P坐标,即可解决问题;②如图3中,当AB为对角线时,AP=BQ,AP∥BQ,求出点P坐标,即可解决问题.
解:(1)如图1,过点D做DP⊥y轴于点P,
∵点E为AD的中点,
∴AE=DE.
又∵DP⊥y轴,∠AOE=90°,
∴∠DPE=∠AEO.
∵在△PDE与△OAE中,
∠DPE=∠AOE,PE=OE,∠PED=∠OEA,
∴△PDE≌△OAE(ASA),
∴PD=OA,
∵A(﹣1,0),
∴PD=1,
∴D(1,4).
∵点D在反比例函数图象上,
∴k=xy=1×4=4.
∵点C在反比例函数图象上,C的坐标为(2,b),
∴b=![]() =2,
=2,
∴a=1,k=4,b=2;
(2)能,点C、D绕点O顺时针旋转180度时,点C′、D′落在y=![]() 图象上.或点C、D关于原点中心对称的点在图象上;
图象上.或点C、D关于原点中心对称的点在图象上;
(3)∵由(1)可知k=4,
∴反比例函数的解析式为y=![]() ,
,
∵点P在y=![]() 上,点Q在y轴上,
上,点Q在y轴上,
∴设Q(0,y),P(x, ![]() ).
).
①当AB为边时,如图1中,若四边形ABPQ为平行四边形,则![]() =0,
=0,
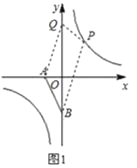
解得x=1,此时P1(1,4),Q1(0,6).
如图2中,若四边形ABQP是平行四边形时,AP=BQ,且AP∥BQ,
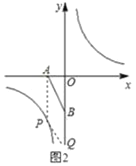
此时P2(﹣1,﹣4),Q2(0,﹣6).
②如图3中,当AB为对角线时,AP=BQ,AP∥BQ,
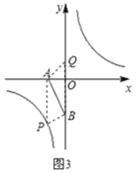
此时P3(﹣1,﹣4),Q3(0,2),
综上所述,满足条件的P、Q坐标分别为P1(1,4),Q1(0,6);P2(﹣1,﹣4),Q2(0,﹣6);P3(﹣1,﹣4),Q3(0,2).
“点睛”本题考查的是反比例函数综合题,涉及到用待定系数法求反比例函数的解析式、平行四边形的性质、全等三角形的判定与性质等相关知识,难度较大.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案【题目】计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如,用十六进制表示:C+F=1B,19﹣F=A,18÷4=6,则A×B=( )
A. 72 B. 6E C. 5F D. B0