题目内容
【题目】已知:正方形ABCD的边长为a,P是边CD上一个动点不与C、D重合,CP=b,以CP为一边在正方形ABCD外作正方形PCEF,连接BF、DF.
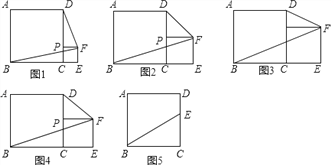
观察计算:(1)如图1,当a=4,b=1时,四边形ABFD的面积为 ;
(2)如图2,当a=4,b=2时,四边形ABFD的面积为 ;
(3)如图3,当a=4,b=3时,四边形ABFD的面积为 ;
探索发现:
(4)根据上述计算的结果,你认为四边形ABFD的面积与正方形ABCD的面积之间有怎样的关系?
综合应用:
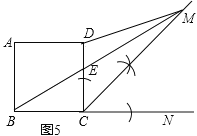
(5)农民赵大伯有一块正方形的土地(如图5),由于修路被占去一块三角形的地方△BCE,但决定在DE的右侧补给赵大伯一块土地,补偿后的土地为四边形ABMD,且四边形ABMD的面积与原来正方形土地的面积相等,M、E、B三点要在一条直线上,请你在图5中画图确定M点的位置.并证明你的结论.
【答案】16 16 16 相等与正方形PCEF的边长无关
【解析】试题分析:
(1)4×4+(1+4)×1÷2-1×5÷2=16;
(2)4×4+(2+4)×2÷2-2×6÷2=16;
(3)4×4+(3+4)×3÷2-3×7÷2=16;
(4)无论点P在CD边上的什么位置,四边形ABFD的面积与正方形ABCD的面积相等,与正方形PCEF的边长无关.
证明:连接BD,CF,
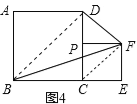
∵四边形ABCD是正方形,
∴∠DBC=45°,
同理∠FCE=45°,
∴BD∥CF,
∴S△BCD=S△BDF,
∴四边形ABFD的面积与正方形ABCD的面积相等;
(5)如图5,作BC的延长线CN,作∠DCN的角平分线交BE的延长线于点M,则四边形ABMD的面积与正方形ABCD的面积相等,点M即为所求.

练习册系列答案
相关题目