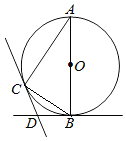题目内容
【题目】如图，BD为正方形ABCD的对角线，BE平分∠DBC，交DC于点E，延长BC到F，使CF＝CE，连接DF.若CE＝1 cm，则BF＝__________．
【答案】(2＋
) cm
【解析】
根据题意得CE=CF，则BF=BC+CF=CD+CE，而CD=DE+CE，关键是求出DE的长；由BE平分∠DBC，∠BCE=90°，可以作辅助线：过点E作EG⊥BD于点G，如图，利用角平分线的性质，得到GE=CE；接下来在等腰直角三角形DGE中，利用勾股定理求出DE的长，即可得出结论.
过点E作EG⊥BD于点G.
∵BE平分∠DBC，
∴GE=CE=1cm.
∵四边形ABCD为正方形，
∴∠GDE=45°.
又∵EG⊥BD，
∴∠EGD=90°，
∴∠GED=∠GDE=45°，
∴DG=GE=1cm.
根据勾股定理，得DE=cm，
∴BC=CD=(+1)cm.
又∵CE=CF，
∴BF=BC+CF=CD+CE=(+2)cm.
故答案为(+2)cm.
练习册系列答案
发散思维新课堂系列答案
相关题目
【题目】某学校的复印任务原来由甲复印社承接，其收费y（元）与复印页数x（页）的关系如下表：
x（页） | 100 | 200 | 400 | 1000 | … |
y（元） | 40 | 80 | 160 | 400 |
（1）若y与x满足初中学过的某一函数关系，求函数的解析式;
（2）现在乙复印社表示：若学校先按每月付给200元的承包费，则可按每页0.15元收费，则乙复印社每月收费y（元）与复印页数x（页）的函数关系为________________，
（3）学校准备复印材料1000页，应选择哪个复印社比较优惠？
