题目内容
图甲是第七届国际数学教育大会的会徽,会徽的主体图案是由图乙中的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1.细心观察图形,认真分析下列各式,然后解答问题:
(
| 1 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
(1)请用含有n(n是正整数)的等式表示上述变化规律,并计算出OA10的长;
(2)求出S12+S22+S32+…+S102的值.
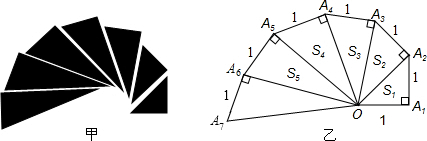
分析:解答此题要熟悉勾股定理,根据定理求出OA1、OA2、OA3、OA4、OA5…OAn的值,得出规律,进一步得出面积的变化规律.
解答:解:(1)根据勾股定理,OA2=
=
,OA3=
,
OA4=2,…,OA10=
,OAn=
=
.
S1=
;S2=
;S3=
;…;S10=
;Sn=
;
(2)S12+S22+S32+…+S102=(
)2+(
)2+(
)2+…+(
)2=
=
.
|
| 2 |
| 3 |
OA4=2,…,OA10=
| 10 |
(
|
| n |
S1=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(2)S12+S22+S32+…+S102=(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1+2+3+…+9+10 |
| 4 |
| 55 |
| 4 |
点评:此题是一道规律探索题,首先进行具体数的计算,根据数字找出规律,得出一般性规律.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 线段的长度为正整数( )
线段的长度为正整数( )
 )2+1=2,S1=
)2+1=2,S1=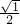 ;(
;( )2+1=3,S2=
)2+1=3,S2= ;(
;( )2+1=4,S3=
)2+1=4,S3= ;…
;…
 ,如果把图乙中的直角三角形继续作下去,那么
,如果把图乙中的直角三角形继续作下去,那么 这些线段中有多少条线段的长度为正整数?
这些线段中有多少条线段的长度为正整数?