题目内容
(1)若 ,求
,求 的值.
的值.(2)已知二次函数图象与x轴交点(2,0),(-1,0),与y轴交点是(0,-1),求此二次函数解析式.
【答案】分析:(1)设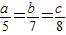 =k,然后用k分别表示a、b、c的值,将它们代入所求的代数式
=k,然后用k分别表示a、b、c的值,将它们代入所求的代数式 消去k即可得到
消去k即可得到 的值;
的值;
(2)可设二次函数的解析式为两点式:y=a(x-2)(x+1)(a≠0),然后将点(0,-1)代入该函数解析式即可求得a的值.
解答:解:(1)设 =k,则a=5k,b=7k,c=8k.
=k,则a=5k,b=7k,c=8k.
当k=0时,即a=b=c=0,则2a-b+3c=0,分式 无意义,故k≠0.
无意义,故k≠0.
所以 =
= =
= =
= ,即
,即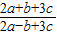 =
= ;
;
(2)∵二次函数图象与x轴交点(2,0),(-1,0),
∴设二次函数的解析式为:y=a(x-2)(x+1)(a≠0),
又∵二次函数图象与y轴交点是(0,-1),
∴-1=a(0-2)(0+1),即-1=-2a,
解得,a= ,
,
∴该二次函数的解析式为y= (x-2)(x+1),或y=
(x-2)(x+1),或y= x2-
x2- x-1.
x-1.
点评:本题考查了比例的性质,待定系数法求二次函数的解析式.二次函数的解析式由三种形式,解答该题时根据已知条件设解析式的形式为两点式.
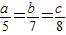 =k,然后用k分别表示a、b、c的值,将它们代入所求的代数式
=k,然后用k分别表示a、b、c的值,将它们代入所求的代数式 消去k即可得到
消去k即可得到 的值;
的值;(2)可设二次函数的解析式为两点式:y=a(x-2)(x+1)(a≠0),然后将点(0,-1)代入该函数解析式即可求得a的值.
解答:解:(1)设
 =k,则a=5k,b=7k,c=8k.
=k,则a=5k,b=7k,c=8k.当k=0时,即a=b=c=0,则2a-b+3c=0,分式
 无意义,故k≠0.
无意义,故k≠0.所以
 =
= =
= =
= ,即
,即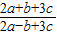 =
= ;
;(2)∵二次函数图象与x轴交点(2,0),(-1,0),
∴设二次函数的解析式为:y=a(x-2)(x+1)(a≠0),
又∵二次函数图象与y轴交点是(0,-1),
∴-1=a(0-2)(0+1),即-1=-2a,
解得,a=
 ,
,∴该二次函数的解析式为y=
 (x-2)(x+1),或y=
(x-2)(x+1),或y= x2-
x2- x-1.
x-1.点评:本题考查了比例的性质,待定系数法求二次函数的解析式.二次函数的解析式由三种形式,解答该题时根据已知条件设解析式的形式为两点式.

练习册系列答案
相关题目
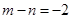 ,求
,求 的值
的值 中,
中, 是
是 的中点,将
的中点,将 沿
沿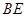 折叠后得到
折叠后得到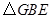 ,且点
,且点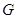 在矩形
在矩形 交
交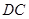 于点
于点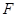

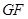 与
与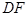 之长是否相等, 并说明理由.
之长是否相等, 并说明理由.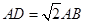 ,求
,求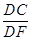 的值.
的值.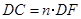 ,求
,求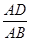 的值.
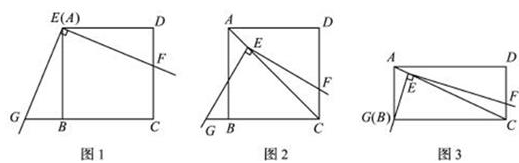
的值.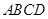 上,使三角板的直角顶点
上,使三角板的直角顶点 与正方形
与正方形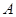 重合,三角扳的一边交
重合,三角扳的一边交 于点
于点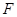 .另一边交
.另一边交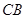 的延长线于点
的延长线于点 .
.
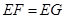 ;
; 的对角线
的对角线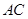 上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由: ,其他条件不变,若
,其他条件不变,若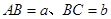 ,求
,求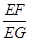 的值.
的值.

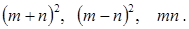
 ,求
,求 的值
的值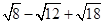
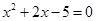 ;
; ,求
,求 的值。
的值。