题目内容
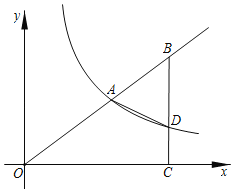
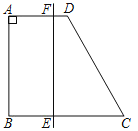
【题目】 如图，在四边形ABCD中，AB⊥AD，AD∥BC，且AB＝BC＝4，AD＝2，点E是边BC上的一个动点，EF⊥BC交AD于点F，将四边形ABCD沿EF所在直线折叠，若两边重叠部分的面积为3，则BE的长为（ ）
A.
或
B.C.D.
或4+
【答案】A
【解析】
如图1，将四边形ABCD沿EF所在直线折叠，两边重叠部分为五边形EB′GDF，推出四边形ABEF是矩形，得到AB=EF=4，AF=BE，根据折叠的性质得到A′F=AF，B′E=BE，A′B′=AB=4，设BE=x，则AF=A′F=B′E=x，根据相似三角形的性质得到B′G=4（2-x），根据题意列方程得到
[（2-x）+（4-x）]×4
（4-2x）（8-4x）=3此方程无实数根，故这种情况不存在；如图2，将四边形ABCD沿EF所在直线折叠，两边重叠部分为矩形A′B′EF，设BE=x，则AF=A′F=B′E=x，根据题意列方程得到BE=
；如图3，将四边形ABCD沿EF所在直线折叠，两边重叠部分为△CEG，设BE=x，则AF=A′F=B′E=x，根据相似三角形的性质得到EG=2（4-x），根据题意列方程得到结论．
解：如图1，将四边形ABCD沿EF所在直线折叠，两边重叠部分为五边形EB′GDF，
∵AB⊥AD，AD∥BC，EF⊥BC，
∴四边形ABEF是矩形，
∴AB＝EF＝4，AF＝BE，
∵将四边形ABCD沿EF所在直线折叠，
∴A′F＝AF，B′E＝BE，A′B′＝AB＝4，
设BE＝x，则AF＝A′F＝B′E＝x，
∴DF＝2﹣x，CE＝4﹣x，
∴A′D＝2x﹣2，CB′＝4﹣2x，
∵A′D∥B′C，
∴△A′DG∽△B′CG，
∴
∴
，
∴B′G＝4（2﹣x），
∵两边重叠部分的面积为3，
∴ [（2﹣x）+（4﹣x）]×4﹣（4﹣2x）（8﹣4x）＝3
此方程无实数根，故这种情况不存在；
如图2，将四边形ABCD沿EF所在直线折叠，两边重叠部分为矩形A′B′EF，
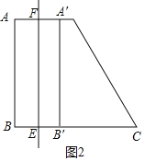
设BE＝x，则AF＝A′F＝B′E＝x，
∵两边重叠部分的面积为3，
∴B′EA′B′＝4x＝3，
解得：x＝，
∴BE＝
；
如图3，将四边形ABCD沿EF所在直线折叠，两边重叠部分为△CEG，
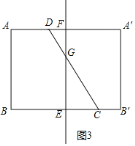
设BE＝x，则AF＝A′F＝B′E＝x，
∴DF＝x﹣2，CE＝4﹣x，
∵DF∥CE，
∴△DFG∽△CEG，
∴
∴
，
∴EG＝2（4﹣x），
∵两边重叠部分的面积为3，
∴×2（4﹣x）（4﹣x）＝3，
解得：x＝4﹣
或x＝4+（不合题意舍去），
综上所述，BE的长为或4﹣，
故选：A．
