题目内容
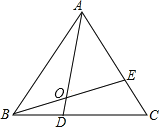
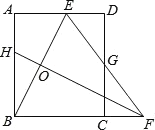
【题目】如图,△ABC中,AB=AC,高BD、CE相交于点O,连接AO并延长交BC于点F,则图中全等的直角三角形共有( )

A. 4对B. 5对C. 6对D. 7对
【答案】C
【解析】
①△BDC≌△CEB,根据等边对等角得:∠ABC=∠ACB,由高得:∠BDC=∠CEB=90°,所以利用AAS可证明全等;
②△BEO≌△CDO,加上对顶角相等,利用AAS可证明全等;
③△AEO≌△ADO,根据HL可证明全等;
④△ABF≌△ACF,根据SAS可证明全等;
⑤△BOF≌△COF,根据等腰三角形三线合一的性质得:BF=FC,∠AFB=∠AFC,利用SAS可证明全等;
⑥△AOB≌△AOC,根据SAS可证明全等;
⑦△ABD≌△ACE,利用AAS可证明全等.
解:有7对全等三角形:
①△BDC≌△CEB,理由是:
∵AB=AC,
∴∠ABC=∠ACB,
∵BD和CE是两腰上的高,
∴∠BDC=∠CEB=90°,
在△BDC和△CEB中,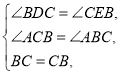
∴△BDC≌△CEB(AAS),
∴BE=DC,
②△BEO≌△CDO,理由是:
在△BEO和△CDO中,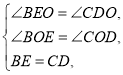
∴△BEO≌△CDO(AAS),
③△AEO≌△ADO,理由是:
由△BEO≌△CDO得:EO=DO,
在Rt△AEO和Rt△ADO中,![]()
∴Rt△AEO≌Rt△ADO(HL),
∴∠EAO=∠DAO,
④△ABF≌△ACF,理由是:
在△ABF和△ACF中,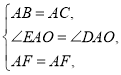
∴△ABF≌△ACF(SAS),
⑤△BOF≌△COF,理由是:
∵AB=AC,∠BAF=∠CAF,
∴BF=FC,∠AFB=∠AFC,
在△BOF和△COF中,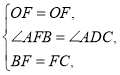
∴△BOF≌△COF(SAS),
⑥△AOB≌△AOC,理由是:
在△AOB和△AOC中,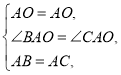
∴△AOB≌△AOC(SAS),
⑦△ABD≌△ACE,理由是:
在△ABD和△ACE中,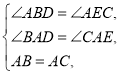
∴△ABD≌△ACE(AAS).
故选:C.

【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收贵的价目表如下(注:水费按月份结算,![]() 表示立方米)
表示立方米)
价目表 | |
每月用水量 | 价格 |
不超过 |
|
超出 |
|
超出 |
|
![]() 某户居民1月份和2月份的用水量分别为
某户居民1月份和2月份的用水量分别为![]() 和
和![]() ,则应收水费分别是 元和 元
,则应收水费分别是 元和 元
![]() 若该户居民
若该户居民![]() 月份用水量
月份用水量![]() (其中
(其中![]() ),则应收水费多少元? (用含
),则应收水费多少元? (用含![]() 的式子表示,并化简)
的式子表示,并化简)
![]() 若该户居民
若该户居民![]() 两个月共用水
两个月共用水 ![]() (
(![]() 月份用水量超过
月份用水量超过![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() 两个月共交水费多少元? (用含
两个月共交水费多少元? (用含 ![]() 的式子表示,并化简)
的式子表示,并化简)