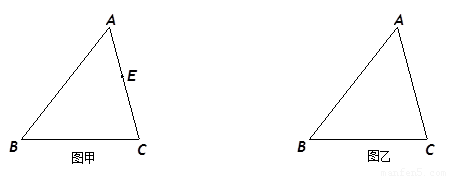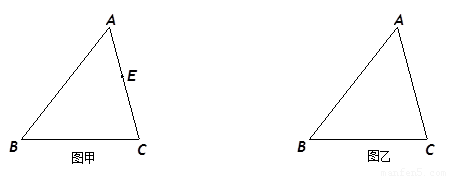题目内容
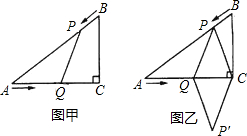
如图甲,在菱形ABCD中,AC与BD交于O,AC=8,AD=5,DE⊥CD,垂足为E,交AC于F.
(1)填空:△ODF∽△
(2)求OF的长;
(3)△DCE沿ED剪下,再把△DCE绕EC翻转,平移拼接成如图乙所示(拼接后D、E两点正好交换位置),判断此时四边形ABDC是什么特殊四边形(不证明)?并求图乙中的AC长.

(1)填空:△ODF∽△
OCD(答案不唯一)
OCD(答案不唯一)
(只写一个三角形);(2)求OF的长;
(3)△DCE沿ED剪下,再把△DCE绕EC翻转,平移拼接成如图乙所示(拼接后D、E两点正好交换位置),判断此时四边形ABDC是什么特殊四边形(不证明)?并求图乙中的AC长.

分析:(1)先由菱形的性质得出∠ACD=∠ACB,由对顶角的性质得出∠AFD=∠CFE,再由直角三角形的性质得出∠ODF=∠ACD,故可得出结论;
(2)先根据AC=8,AD=5求出OD的长,由(1)可知△ODF∽△OCD,再由相似三角形的对应边成比例即可得出OF的长;
(3)先根据菱形的性质判断出四边形ABDC的形状,再得出DE的长,在Rt△DEC中利用勾股定理可求出CE的长,故可得出AC的长.
(2)先根据AC=8,AD=5求出OD的长,由(1)可知△ODF∽△OCD,再由相似三角形的对应边成比例即可得出OF的长;
(3)先根据菱形的性质判断出四边形ABDC的形状,再得出DE的长,在Rt△DEC中利用勾股定理可求出CE的长,故可得出AC的长.
解答:解:(1)∵四边形ABCD是菱形,
∴∠ACD=∠ACB,
∵DE⊥BC,
∴∠ACB+∠CFE=90°,
∵∠DFO+∠ODF=90°,∠CFE=∠DFE,
∴∠ODF=∠ACB,
∴∠ODF=∠ACD,
∴:△ODF∽△OCD,
故答案为:△OCD(答案不唯一);
(2)在菱形ABCD中,
∵BD⊥AC,AC=8,AD=5,
∴OA=4,OD=3,
由(1)知,△ODF∽△OCD,
∴
=
,即32=4×OF,解得,OF=
;
(3)在图乙中,
∵AC∥BD,AB=CD,
∴四边形ABCD是等腰梯形,
∵DE•BC=
AC•BD=
×6×8,解得DE=
,
在Rt△DEC中,
∵DE2+CE2=CD2,即(
)2+CE2=25,解得CE=
,
∴AC=AE+CE=5+
=
.
∴∠ACD=∠ACB,
∵DE⊥BC,
∴∠ACB+∠CFE=90°,
∵∠DFO+∠ODF=90°,∠CFE=∠DFE,
∴∠ODF=∠ACB,
∴∠ODF=∠ACD,
∴:△ODF∽△OCD,
故答案为:△OCD(答案不唯一);
(2)在菱形ABCD中,
∵BD⊥AC,AC=8,AD=5,
∴OA=4,OD=3,
由(1)知,△ODF∽△OCD,
∴
| OD |
| OC |
| OF |
| OD |
| 9 |
| 4 |
(3)在图乙中,
∵AC∥BD,AB=CD,
∴四边形ABCD是等腰梯形,
∵DE•BC=
| 1 |
| 2 |
| 1 |
| 2 |
| 24 |
| 5 |
在Rt△DEC中,
∵DE2+CE2=CD2,即(
| 24 |
| 5 |
| 7 |
| 5 |
∴AC=AE+CE=5+
| 7 |
| 5 |
| 32 |
| 5 |
点评:本题考查的是相似三角形综合题,涉及到相似三角形的判定与性质、勾股定理、菱形的性质等相关知识,熟知菱形的知识是解答此题的关键.

练习册系列答案
相关题目