Question

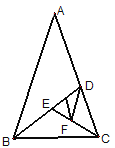
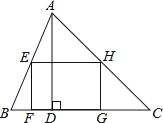
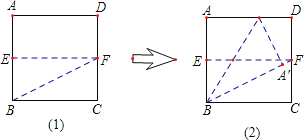
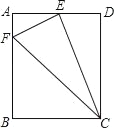
【题目】已知：如图，在矩形ABCD中，E为AD的中点，EF⊥EC交AB于F（AB＞AE）.问：△AEF与△EFC是否相似？若相似，证明你的结论；若不相似，请说明理由.

Answer 1

【答案】相似,理由见解析.

【解析】

延长FE和CD交于P，求出等腰三角形PCF，推出∠PCE=∠FCE，根据△AFE∽△DEC推出∠AEF=∠PCE，推出∠A=∠FEC，∠AEF=∠ECF，根据相似三角形的判定推出即可．

答：相似．

证明：延长FE和CD交于P，

∵四边形ABCD是矩形，

∴∠A=∠ADC=∠EDP=90°，

∵E为AD中点，

∴AE=DE，

在△AFE和△DPE中， ，

∴△AFE≌△DPE（ASA），

∴PE=EF，

∵EC⊥EF，

∴PC=FC，

∴∠PCE=∠FCE，

∵CE⊥EF，∠A=90°，

∴∠FEC=90°，

∴∠AEF+∠DEC=90°，∠AEF+∠AFE=90°，

∴∠AFE=∠DEC，

即∠A=∠EDC，∠AFE=∠DEC，

∴△AFE∽△DEC，

∴∠AEF=∠DCE，

∵∠DCE=∠FCE，

∴∠AEF=∠ECF，

∵∠A=∠FEC=90°，

∴△AFE∽△EFC．