题目内容
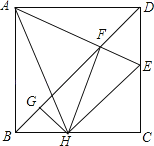
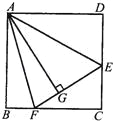
【题目】如图,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF,垂足为G,且AG=AB,则∠EAF为多少度.
【答案】45°
【解析】试题分析:
由四边形ABCD是正方形可结合AG⊥EF可得∠B=∠AGF=∠AGE=∠D=90°,结合AB=AG=AD,可得△ABF≌△AGF,△ADE≌△AGE,从而可得∠BAF=∠GAF,∠DAE=∠GAE,结合∠BAD=90°即可得到∠EAF=45°.
试题解析:
在Rt△ABF与Rt△AGF中,∵AB=AG,AF=AF,∠B=∠G=90°,
∴△ABF≌△AGF(HL),
∴∠BAF=∠GAF,
同理易得:△AGE≌△ADE,有∠GAE=∠DAE;
即∠EAF=∠EAG+∠FAG=![]() ∠DAG+
∠DAG+![]() ∠BAG=
∠BAG=![]() ∠DAB=45°,
∠DAB=45°,
故∠EAF=45°.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目