Question

【题目】已知：正方形ABCD的边长为4cm，点E从点A出发沿AD方向以1cm/秒的速度运动，与此同时，点F也从点D出发沿DC方向相同的速度运动，记运动的时间为t（0≤t≤4），AF与BE交于P点．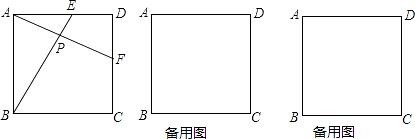
（1）如图，在运动过程中，AF与BE相等吗？请说明理由．
（2）在运动过程中，要使得△BPC是等腰三角形，t应为何值？请画出图形，并求出所有满足条件的t值．

Answer 1

【答案】
（1）解：结论：AF=BE，

证明：如图1中，

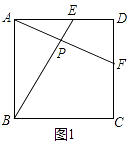
∵四边形ABCD是正方形，

∴AB=AD，∠BAE=∠D=90°，

在△ABE和△DAF中，

，

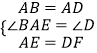∴△ABE≌△DAF，

∴BE=AF．

（2）解：①如图2中，

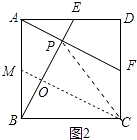
当CP=CB时，作CM⊥BE垂足为O，交AB于M．

∵△ABE≌△DAF，

∴∠ABE=∠DAF，

∵∠ABE+∠AEB=90°，

∴∠DAF+∠AEB=90°

∴∠APE=90°，

∴AF⊥BE，

∴OM∥AP，

∵OP=OB，

∴AM=BM，

∵∠ABE+∠AEB=90°∠ABE+∠CMB=90°，

∴∠AEB=∠CMB，

在△ABE和△CBM中，

，

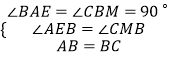∴△ABE≌△CBM，

∴AE=BM=2，

∴t=2，

②如图3中，

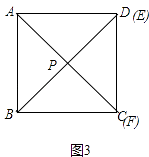
当点E运动到与点D重合，点F运动到与点C重合时，△PBC是等腰三角形，此时t=4，

③当t=0时，点E在点A处，点F在点D处，则AF于BE的交点P于点A重合，此时，△BPC显然是等腰直角三角形

∴t=0或2或4时，△BPC是等腰三角形

【解析】（1）结论：AF=BE，只要证明△ABE≌△DAF即可．（2）分两种情形讨论：①如图2中，当CP=CB时，作CM⊥BE垂足为O，交AB于M，先证明AM=BM，再证明△ABE≌△CBM即可，②如图3中，当点E运动到与点D重合，点F运动到与点C重合时，△PBC是等腰三角形，求出t即可．
【考点精析】关于本题考查的等腰三角形的判定和正方形的性质，需要了解如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案．