题目内容
【题目】如图，A，B是直线l上的两点，AB=4厘米，过l外一点C作CD∥l，射线BC与l所组成的锐角为60°，线段BC=2厘米，动点P、Q分别从B、C同时出发，P以1厘米/秒的速度，沿由B向C的方向运动；Q以2厘米/秒的速度，沿由C向D的方向运动，设P、Q运动的时间为t秒，当t＞2时，PA交CD于点E． 
（1）用含t的代数式分别表示CE和QE的长；
（2）求△APQ的面积s与t的函数表达式；
（3）当QE恰好平分△APQ的面积时，QE的长是多少？
【答案】
（1）解：由题意知：BP=t，CQ=2t，PC=t﹣2．
∵EC∥AB，
∴ 
= 
，
∴EC= 
= 
，
∴QE=QC﹣EC=2t﹣ = 
；
（2）解：如图，作PF⊥L于F，交DC延长线于M，AN⊥CD于N．
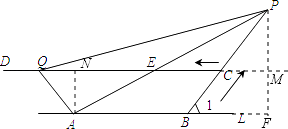
在△PBF中，PF=PBsin60°= 
t，
∴S△APQ=S△AQE+S△PQE
= 
QEAN+ QEPM= QEPF
= × × t= （t2﹣2t+4）；
（3）解：此时，E为PA的中点，所以C也是PB的中点，
则t﹣2=2，
∴t=4，
∴QE= = 
=6（厘米）．
【解析】（1）根据题意得出BP=t，CQ=2t，PC=t﹣2，再根据EC∥AB，得出 = ，最后得出EC的值，即可表示出CE和QE的长；（2）以QE为底边，过P引l的垂线作高，根据P的速度可以用t表示出BP，也就能用BP和∠1的正弦函数求出高，那么关键是求QE的长，我们可以根据Q的速度用时间t表示出CQ，那么只要求出CE即可．用相似三角形的对应线段成比例来求CE的长，根据三角形PEC和三角形PAB相似，可得出关于CE、AB、PC、BC的比例式，由BP、BC、AB的值，可以用含t的式子表示出CE，也就表示出了QE，那么可根据三角形的面积公式，得出关于S与t的函数关系式；（3）如果QE恰好平分三角形APQ的面积，那么此时P到CD和CD到l之间的距离就相等，那么C就是PB的中点，可根据BP=2BC求出t的值，然后根据（1）中得出的表示QE的式子，将t代入即可得出QE的值即可．
【考点精析】通过灵活运用相似三角形的判定与性质和解直角三角形，掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)即可以解答此题．
