题目内容
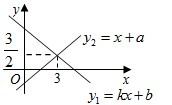 一次函数y1=kx+b与y2=x+a的图象如图,下列结论中:
一次函数y1=kx+b与y2=x+a的图象如图,下列结论中:(1)二元一次方程组
|
|
(2)关于x的不等式x+a>kx+b的解集为x<3;
(3)k<0,b>0;
(4)x>0时y2>-1.5;
正确的是
分析:结合一次函数的性质、一次函数与不等式的关系,根据图象观察,得出结论.
解答:解:由于函数图象交点坐标为两函数解析式组成的方程组的解,可得出(1)的结论正确;
由图知:当x<3时,函数y1图象对应的点都在y2的图象上方,因此当x<3时,y2<y1,因此(2)的结论不正确;
由图知:y1的函数值y随x的增大而减小,且函数交y轴于正半轴,因此k<0,b>0,(3)正确;
由图知:两函数的交点坐标为(3,1.5),代入y2中,可求得a=-1.5;因此一次函数y2与y轴的交点坐标为(0,-1.5),由于函数y2的函数值随x的增大而增大,因此当x>0时,y2>-1.5;所以(4)的结论正确.
因此本题共有3个正确的结论:(1)(3)(4).
由图知:当x<3时,函数y1图象对应的点都在y2的图象上方,因此当x<3时,y2<y1,因此(2)的结论不正确;
由图知:y1的函数值y随x的增大而减小,且函数交y轴于正半轴,因此k<0,b>0,(3)正确;
由图知:两函数的交点坐标为(3,1.5),代入y2中,可求得a=-1.5;因此一次函数y2与y轴的交点坐标为(0,-1.5),由于函数y2的函数值随x的增大而增大,因此当x>0时,y2>-1.5;所以(4)的结论正确.
因此本题共有3个正确的结论:(1)(3)(4).
点评:本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.

练习册系列答案
相关题目
 14、一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:
14、一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论: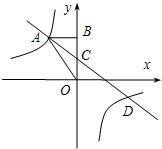 如图,已知一次函数y1=kx+b(k≠0)与反比例函数
如图,已知一次函数y1=kx+b(k≠0)与反比例函数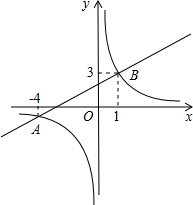 ,3)两点.
,3)两点. 如图,A(-3,n)、B(2,-3)是一次函数y1=kx+b的图象和反比例函数y2=
如图,A(-3,n)、B(2,-3)是一次函数y1=kx+b的图象和反比例函数y2= 如图,已知一次函数y1=kx+b的图象与反比例函数y2=
如图,已知一次函数y1=kx+b的图象与反比例函数y2=