题目内容
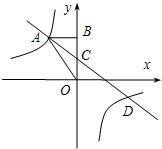 如图,已知一次函数y1=kx+b(k≠0)与反比例函数y2=
如图,已知一次函数y1=kx+b(k≠0)与反比例函数y2=| m | x |
分析:根据题意S△AOB=1,可得m的值,又由CO=BC=1,且反比例函数的图象在二、四象限,可得关于k、b的关系式,解可得答案.
解答: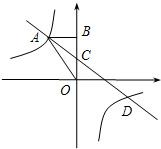 解:依题意有:S△AOB=
解:依题意有:S△AOB=
AB•OB=
xy=1,
即
|m|=1,
∴m=±2,
又∵反比例函数的图象在二、四象限,
∴y2=
∵CO=BC=1,
∴OB=2,
∴AB=1,
∴A(-1,2),C(0,1),
∴
,
解得
,
∴y1=-x+1.
故答案为:y1=-x+1,y2=
.
 解:依题意有:S△AOB=
解:依题意有:S△AOB=| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
∴m=±2,
又∵反比例函数的图象在二、四象限,
∴y2=
| -2 |
| x |
∵CO=BC=1,
∴OB=2,
∴AB=1,
∴A(-1,2),C(0,1),
∴
|
解得
|
∴y1=-x+1.
故答案为:y1=-x+1,y2=
| -2 |
| x |
点评:本题考查了反比例函数的图象的性质以及其与直线的关系,利用形数结合解决此类问题,是非常有效的方法.

练习册系列答案
相关题目
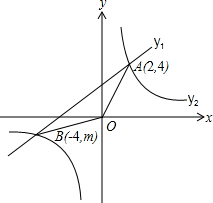 B(-4,m)两点.
B(-4,m)两点. 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=- (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数 如图,已知一次函数y=kx+b的图象交反比例函数
如图,已知一次函数y=kx+b的图象交反比例函数