题目内容
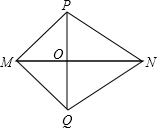 如图,MP=MQ,PN=QN,MN交PQ于点O,则下列结论中不正确的是
如图,MP=MQ,PN=QN,MN交PQ于点O,则下列结论中不正确的是
- A.△MPN≌△MQN
- B.OP=OQ
- C.MO=NO
- D.∠MPN=∠MQN
C
分析:由已知条件中两边对应相等加上公共边很容易得到△MPN≌△MQN,可得∠MPN=∠MQN,进而可得△PON≌△QON可得OP=OQ
于是答案可得.
解答:∵MP=MQ,PN=QN,PQ=PQ
∴△MPN≌△MQN
故A正确;
∵MN垂直平分PQ
∴OP=OQ
故B正确;
∴∠MPN=∠MQN
故D正确.
∴只有C是错误的.
故选C.
点评:本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.做题时,要结合已知条件与全等的判定方法对选项逐一验证.
分析:由已知条件中两边对应相等加上公共边很容易得到△MPN≌△MQN,可得∠MPN=∠MQN,进而可得△PON≌△QON可得OP=OQ
于是答案可得.
解答:∵MP=MQ,PN=QN,PQ=PQ
∴△MPN≌△MQN
故A正确;
∵MN垂直平分PQ
∴OP=OQ
故B正确;
∴∠MPN=∠MQN
故D正确.
∴只有C是错误的.
故选C.
点评:本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.做题时,要结合已知条件与全等的判定方法对选项逐一验证.

练习册系列答案
相关题目
 41、如图,MP=MQ,PN=QN,MN交PQ于点O,则下列结论中不正确的是( )
41、如图,MP=MQ,PN=QN,MN交PQ于点O,则下列结论中不正确的是( ) 10、如图,MP⊥NP,MQ为∠PMN的平分线,MT=MP,连接TQ,则下列结论中不正确的是( )
10、如图,MP⊥NP,MQ为∠PMN的平分线,MT=MP,连接TQ,则下列结论中不正确的是( ) 6、如图,MP=MQ,只要再具备一个条件:
6、如图,MP=MQ,只要再具备一个条件: 如图,MP=MQ,只要再具备一个条件:________,就能使△MPN≌△MQN.
如图,MP=MQ,只要再具备一个条件:________,就能使△MPN≌△MQN.