Question

【题目】如图，以△ABC的一边AB为直径作⊙O， ⊙O与BC边的交点D恰好为BC的中点，过点D作⊙O的切线交AC边于点E．

(1) 求证：DE⊥AC；

(2) 连结OC交DE于点F，若，求的值．

Answer 1

【答案】（1）证明见解析（2）

【解析】

试题分析：（1）连接OD，根据三角形的中位线定理可求出OD∥AC，根据切线的性质可证明DE⊥OD，进而得证．

（2）过O作OF⊥BD，根据等腰三角形的性质及三角函数的定义用OB表示出OF、CF的长，根据三角函数的定义求解．

试题解析：(1)连接OD . ∵DE是⊙O的切线，

∴DE⊥OD，即∠ODE=90° .

∵AB是⊙O的直径，

∴O是AB的中点.

又∵D是BC的中点， .

∴OD∥AC .

∴∠DEC=∠ODE= 90° .

∴DE⊥AC .

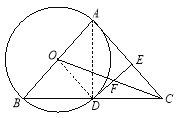
(2)连接AD . ∵OD∥AC，

∴.

∵AB为⊙O的直径， ∴∠ADB= ∠ADC =90° .

又∵D为BC的中点，

∴AB=AC.

∵sin∠ABC= =， 故设AD= 3x , 则AB=AC=4x , OD= 2x .

∵DE⊥AC， ∴∠ADC= ∠AED= 90°.

∵∠DAC= ∠EAD， ∴△ADC∽△AED.

∴.

∴.

∴. ∴.

∴.