Question

【题目】在矩形ABCD中，AB＝6，AD＝8，点E是对角线BD上一动点．

（1）如图1，当CE⊥BD时，求DE的长；

（2）如图2，作EM⊥EN分别交边BC于M，交边CD于N，连MN．

①若，求tan∠ENM；

②若E运动到矩形中心O，连CO．当CO将△OMN分成两部分面积比为1：2时，直接写出CN的长．

Answer 1

【答案】（1）；（2）①；②或．

【解析】

（1）由矩形性质可求得对角线BD＝10，由CE⊥BD得∠CED＝∠BCD＝90°，再由公共角∠CDE＝∠BDC得△CDE∽△BDC，由对应边成比例并把数值代入即求得DE的长．

（2）①由和BD＝10求得DE＝，BE＝．分别过点M、N作BD的垂线段MF、NG，设MF＝a，NG＝b，易证△FBM∽△CBD和△GDN∽△CDB，利用对应边成比例得到用a表示BF、用b表示DG的式子，进而得到用a表示的EF、用b表示的EG．又由EM⊥EN易证△EMF∽△NEG，得到，利用后两个比值把含a、b的式子代入求得a与b之间的关系，再代回去即求得tan∠ENM＝的值．

②先由①的证明过程求得；过点M作MP⊥OC于点P，过点N作NQ⊥OC于点Q，构造△MOP∽△ONQ，所以有．易证△NCQ∽△BDC，设CN＝5x，则可利用对应边成比例得到NQ＝4x、CQ＝3x，进而得OQ＝5﹣3x．CO将△OMN分成△OMH和△ONH，两部分面积比为1：2，若以OH为底，则他们的高MP和NQ的比为1：2或2：1，进而可用x表示MP的长．把用x表示的MP、OQ代入，即求得x的值，进而得CN的长．

解：（1）∵矩形ABCD中，AB＝6，AD＝8

∴∠BCD＝90°，BC＝AD＝8，CD＝AB＝6

∴BD＝＝10

∵CE⊥BD

∴∠CED＝∠BCD＝90°

∵∠CDE＝∠BDC

∴△CDE∽△BDC

∴

∴DE＝

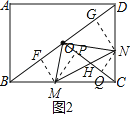
（2）①如图1，过点M作MF⊥BD于点F，过点N作NG⊥BD于点G

∵，BD＝10

∴BD＝BE+DE＝3DE+DE＝4DE＝10

∴DE＝，BE＝

设MF＝a，NG＝b

∵∠BFM＝∠C＝90°，∠FBM＝∠CBD

∴△FBM∽△CBD

∴

∴BF＝＝a

∴EF＝BE﹣BF＝a

同理可证：△GDN∽△CDB

∴

∴DG＝＝b

∴EG＝DE﹣DG＝b

∵EM⊥EN

∴∠MEN＝∠MFE＝∠NGE＝90°

∴∠MEF+∠NEG＝∠MEF+∠EMF＝90°

∴∠EMF＝∠NEG

∴△EMF∽△NEG

∴

∴EFEG＝NGMF

∴（a）（b）＝ba

整理得：16a＝90﹣27b

∴在Rt△MEN中，tan∠ENM＝＝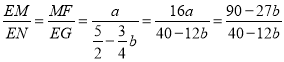

②如图2，过点M作MF⊥BD于点F，MP⊥OC于点P，过点N作NG⊥BD于点G，NQ⊥OC于点Q，设OC与MN交点为H

∵点O为矩形中心，BD＝10

∴OB＝OD＝OC＝BD＝5

由①可得，设MF＝a，NG＝b，则BF＝＝a，DG＝＝b，OFOG＝NGMF

∴OF＝OB﹣BF＝5﹣a，OG＝OD﹣DG＝5﹣b

∴（5﹣a）（5﹣b）＝ab

整理得：16a＝60﹣9b

∴＝

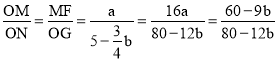设CN＝5x

∵∠NCQ＝∠BDC，∠NQC＝∠BCD＝90°

∴△NCQ∽△BDC

∴＝

∴CQ＝CN＝3x，NQ＝CN＝4x

∴OQ＝OC﹣CQ＝5﹣3x

∵∠MPO＝∠MON＝∠OQN＝90°

∴∠MOP+∠NOQ＝∠NOQ+∠ONQ＝90°

∴∠MOP＝∠ONQ

∴△MOP∽△ONQ

∴

（i）若S△OMH＝2S△ONH，且两三角形都以OH为底

∴MP＝2NQ＝8x

∴

解得：x＝

∴CN＝

（ii）若2S△OMH＝S△ONH，则MP＝NQ＝2x

∴

解得：x＝

∴CN＝

综上所述，CN的长为或．