题目内容
某商场经营一批进价2元一件的小商品,在市场销售中发现此商品日销售单价x(元)与日销售量y(件)之间有如下关系:
小题1:求日销售量y(件)与日销售单价x(元)之间的函数关系式
小题2:设经营此商品的日销售利润为P(元),根据日销售规律:
①试求出日销售利润P(元)与日销售单价x之间的关系式,并求出日销售单价x为多少时,才能获得最大日销售利润,日销售利润P是否存在最小值?若存在,试求出,若不存在,请说明理由
②分别写出x和P的取值范围。
| x | 3 | 5 | 9 | 11 |
| y | 18 | 14 | 6 | 2 |
小题1:求日销售量y(件)与日销售单价x(元)之间的函数关系式
小题2:设经营此商品的日销售利润为P(元),根据日销售规律:
①试求出日销售利润P(元)与日销售单价x之间的关系式,并求出日销售单价x为多少时,才能获得最大日销售利润,日销售利润P是否存在最小值?若存在,试求出,若不存在,请说明理由
②分别写出x和P的取值范围。
小题1:y=-2x+24(0≤x<12)
小题2:①当x=7时,日销售利润获得最大值,为50元。②X的取值范围为x≥0, P的取值范围为 -48≤P≤50
解:(1)设此直线的解析式为y=kx+b
则由A(3,18),B(5,14),得

 3k+b=18 解得 k=-2
3k+b=18 解得 k=-2
5k+b=14 b=24
∴y=-2x+24
将C(9,6)D(11,2)代入y=-2x+24中验证,
满足这个解析式
∴y=-2x+24(0≤x<12),且x=12时,y=0.
(2)①P=y(x-2)=(-2x+24)(x-2)=-2
当x=7时,日销售利润获得最大值,为50元。
②X的取值范围为x≥0, P的取值范围为 -48≤P≤50
则由A(3,18),B(5,14),得

 3k+b=18 解得 k=-2
3k+b=18 解得 k=-25k+b=14 b=24
∴y=-2x+24
将C(9,6)D(11,2)代入y=-2x+24中验证,
满足这个解析式
∴y=-2x+24(0≤x<12),且x=12时,y=0.
(2)①P=y(x-2)=(-2x+24)(x-2)=-2

当x=7时,日销售利润获得最大值,为50元。
②X的取值范围为x≥0, P的取值范围为 -48≤P≤50

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 ),请将上述的6个点按下列的要求分成两类,并写出同类点具有而另一类点不具有的一个特征(请将答案按下列要求写在横线上:特征不能用否定形式表述,点用字母表示。)①甲类含两个点,乙类含其余四个点
),请将上述的6个点按下列的要求分成两类,并写出同类点具有而另一类点不具有的一个特征(请将答案按下列要求写在横线上:特征不能用否定形式表述,点用字母表示。)①甲类含两个点,乙类含其余四个点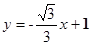 和x轴、y轴分别交于点A、B.,若以线段AB为边作等边三角形ABC,则点C的坐标是 .
和x轴、y轴分别交于点A、B.,若以线段AB为边作等边三角形ABC,则点C的坐标是 .
 的解析式为
的解析式为 ,交
,交 、
、 轴分别于
轴分别于 、
、 两点,点
两点,点 在直线
在直线 为原点
为原点
 在
在 ,则
,则 ▲ ;
▲ ; 在
在 绕点
绕点 得到线段
得到线段 ,
, 恰好在直线
恰好在直线


 的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数
的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数 的图象于Q,
的图象于Q, ,则Q点的坐标为_____________
,则Q点的坐标为_____________