题目内容
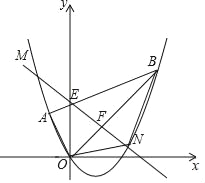
【题目】如图,平面直角坐标系xOy中点A的坐标为(﹣1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.
(1)求点E的坐标;
(2)求抛物线的函数解析式;
(3)点F为线段OB上的一个动点(不与点O、B重合),直线EF与抛物线交于M、N两点(点N在y轴右侧),连接ON、BN,当四边形ABNO的面积最大时,求点N的坐标并求出四边形ABNO面积的最大值.
【答案】(1)E点坐标为(0,![]() );(2)
);(2)![]() ;(3)四边形ABNO面积的最大值为
;(3)四边形ABNO面积的最大值为![]() ,此时N点坐标为(
,此时N点坐标为(![]() ,
,![]() ).
).
【解析】
(1)先利用待定系数法求直线AB的解析式,与y轴的交点即为点E;
(2)利用待定系数法抛物线的函数解析式;
(3)先设N(m,![]() m2
m2![]() m)(0<m<3),则G(m,m),根据面积和表示四边形ABNO的面积,利用二次函数的最大值可得结论.
m)(0<m<3),则G(m,m),根据面积和表示四边形ABNO的面积,利用二次函数的最大值可得结论.
(1)设直线AB的解析式为y=mx+n,
把A(-1,1),B(3,3)代入得![]() ,解得
,解得![]() ,
,
所以直线AB的解析式为y=![]() x+
x+![]() ,
,
当x=0时,y=![]() ×0+
×0+![]() =
=![]() ,
,
所以E点坐标为(0,![]() );
);
(2)设抛物线解析式为y=ax2+bx+c,
把A(-1,1),B(3,3),O(0,0)代入得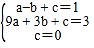 ,解得
,解得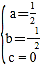 ,
,
所以抛物线解析式为y=![]() x2
x2![]() x;
x;
(3)如图,作NG∥y轴交OB于G,OB的解析式为y=x,
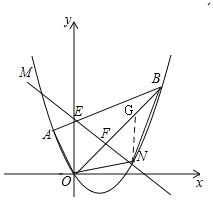
设N(m,![]() m2
m2![]() m)(0<m<3),则G(m,m),
m)(0<m<3),则G(m,m),
GN=m(![]() m2
m2![]() m)=
m)=![]() m2+
m2+![]() m,
m,
S△AOB=S△AOE+S△BOE=![]() ×
×![]() ×1+
×1+![]() ×
×![]() ×3=3,
×3=3,
S△BON=S△ONG+SBNG=![]() 3(
3(![]() m2+
m2+![]() m)=
m)=![]() m2+
m2+![]() m
m
所以S四边形ABNO=S△BON+S△AOB=![]() m2+
m2+![]() m+3=
m+3=![]() (m
(m![]() )2+
)2+![]()
当m=![]() 时,四边形ABNO面积的最大值,最大值为
时,四边形ABNO面积的最大值,最大值为![]() ,此时N点坐标为(
,此时N点坐标为(![]() ,
,![]() ).
).

练习册系列答案
相关题目