题目内容
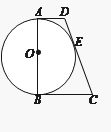
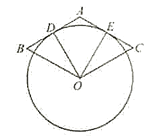
【题目】已知AB是半径为1的圆O的一条弦,且AB=a<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB=a,DC的延长线交圆O于点E,则AE的长为( )
A. ![]() B. 1 C.
B. 1 C. ![]() D. a
D. a
【答案】B
【解析】
试题此题可通过证△EAC≌△OAB,得AE=OA,从而求出EA的长;
△EAC和△OAB中,已知的条件只有AB=AC;由AB=BD,得![]() =
=![]() ,可得∠AED=∠AOB;
,可得∠AED=∠AOB;
四边形ABDE内角于⊙O,则∠EAB+∠D=180°,即∠EAC=180°﹣60°﹣∠D=120°﹣∠D;而∠ECA=180°﹣∠ACB﹣∠BCD=120°﹣∠BCD,上述两个式子中,由BD=AB=BC,易证得∠D=∠BCD,则∠ECA=∠EAC,即△EAC、△OAB都是等腰三角形,而两个等腰三角形的顶角相等,且底边AC=AB,易证得两个三角形全等,由此得解.
解:∵△ABC是等边三角形,
∴AB=BC=AC=BD=a,∠CAB=∠ACB=60°;
∵AB=BD,
∴![]() ,
,
∴∠AED=∠AOB;
∵BC=AB=BD,
∴∠D=∠BCD;
∵四边形EABD内接于⊙O,
∴∠EAB+∠D=180°,即∠EAC+60°+∠D=180°;
又∵∠ECA+60°+∠BCD=180°,
∴∠ECA=∠EAC,即△EAC是等腰三角形;
在等腰△EAC和等腰△OAB中,∠AEC=∠AOB,
∵AC=AB,
∴△EAC≌△OAB;
∴AE=OA=1.
故选B.

练习册系列答案
相关题目