Question

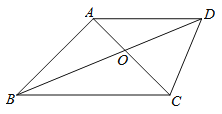
【题目】如图，四边形ABCD中，对角线AC，BD相交于点O，AB=AC=AD，∠DAC=∠ABC．

（1）求证：BD平分∠ABC；

（2）若∠DAC=45°，OA=1，求OC的长．

Answer 1

【答案】（1）证明见解析； （2）

【解析】试题分析：

(1)由题设可知△ABC，△ABD是等腰三角形，证明AD∥BC，再由基本图形“平行线+等腰三角形→角平分线”求证.

(2)可条件可证∠BAC=90°，又因为BD平分∠ABC，故联想过点O作OE⊥BC，得等腰直角△ECO，由角平分线的性质定理得OE=OA，即可求解.

试题解析：

(1)因为AB=AC，AB=AD，所以∠ABC=∠ACB，∠ABD=∠ADB.

因为∠DAC=∠ABC，所以∠DAC=∠ACB，

所以AD∥BC，所以∠ADB=∠CBD，

所以∠ABD=∠CBD，所以BD平分∠ABC.

(2)过点O作OE⊥BC于点E.

因为∠DAC=45°，所以∠ABC=∠ACB=45°，所以∠BAC=90°.

因为BD平分∠ABC，所以OA=OE.

在Rt△OCE中，OE=CE=OA=1，所以OC=.