题目内容
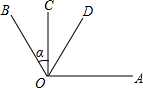 已知:如图,∠AOC=90°,∠COB=α,OD平分∠AOB.求∠COD的大小?
已知:如图,∠AOC=90°,∠COB=α,OD平分∠AOB.求∠COD的大小?
分析:首先根据平分线的定义可得∠AOD=∠BOD=
∠AOB,再求出∠AOB,表示出∠BOD,根据图形得∠COD=∠BOD-∠COB,代入数即可得到答案.
| 1 |
| 2 |
解答:解:∵OD平分∠AOB.
∴∠AOD=∠BOD=
∠AOB,
∵∠AOC=90°,∠COB=α,
∴∠AOB=90°+α,
∴∠BOD=(90°+α)÷2=45°+
α,
∴∠COD=∠BOD-∠COB=45°+
α-α=45°-
α.
∴∠AOD=∠BOD=
| 1 |
| 2 |
∵∠AOC=90°,∠COB=α,
∴∠AOB=90°+α,
∴∠BOD=(90°+α)÷2=45°+
| 1 |
| 2 |
∴∠COD=∠BOD-∠COB=45°+
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了角平分线的定义,以及角的和差关系,解题的关键是理清角之间的关系.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
已知,如图,∠AOC=∠DOE=90°.如果∠AOE=65°,那么∠COD的度数是( ).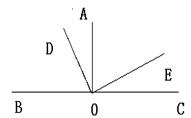
| A.900 | B.1150 | C.1200 | D. 1350 |
 22、证明:角的平分线上的点到角的两边的距离相等.
22、证明:角的平分线上的点到角的两边的距离相等.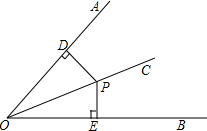 (1)用文字写出角的平分线的性质:
(1)用文字写出角的平分线的性质: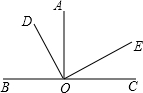 已知,如图,∠AOC=∠DOE=90°.如果∠AOE=65°,那么∠COD的度数是( )
已知,如图,∠AOC=∠DOE=90°.如果∠AOE=65°,那么∠COD的度数是( )