题目内容

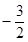已知：抛物线（a≠0）的顶点M的坐标为（1,－2）与y轴交于点C（0，），与x轴交于A、B两点（A在B的左边）.

（1）求此抛物线的表达式；
（2）点P是线段OB上一动点（不与点B重合），点Q在线段BM上移动且∠MPQ＝45°，设线段OP＝x，MQ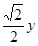＝1，求y1与x的函数关系式，并写出自变量x的取值范围；
（3）①在（2）的条件下是否存在点P，使△PQB是PB为底的等腰三角形，若存在试求点Q的坐标，若不存在说明理由；
②在（1）中抛物线的对称轴上是否存在点F，使△BMF是等腰三角形，若存在直接写出所有满足条件的点F的坐标.

（1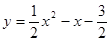）（2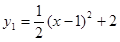）（0≤x＜3）（3）①存在，Q的坐标为（2，1）②F1（1，0），F2（1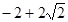，），F3（1，），F4（1，2）.

解析

练习册系列答案
相关题目
已知一抛物线与x轴的交点是A（-1，0）、B（m，0）且经过第四象限的点C（1，n），而m+n=-1，mn=-12，求此抛物线的解析式．
已知：抛物线y=x2-（2m+4）x+m2-10与x轴交于A、B两点，C是抛物线的顶点．
（1）用配方法求顶点C的坐标（用含m的代数式表示）；
（2）“若AB的长为2
2
，求抛物线的解析式．”解法的部分步骤如下，补全解题过程，并简述步骤①的解题依据，步骤②的解题方法；
解：由（1）知，对称轴与x轴交于点D（
 
，0）
∵抛物线的对称性及AB=2
2
，
∴AD=DB=|xA-xD|=2
2
．
∵点A（xA，0）在抛物线y=（x-h）2+k上，
∴0=（xA-h）2+k①
∵h=xC=xD，将|xA-xD|=
2
代入上式，得到关于m的方程0=(
2
)2+(      )②
（3）将（2）中的条件“AB的长为2
2
”改为“△ABC为等边三角形”，用类似的方法求出此抛物线的解析式．
已知：抛物线y=x2-6x+c的最小值为1，那么c的值是（　　）
A、10B、9C、8D、7
已知抛物线y=x2-4x+1，将此抛物线沿x轴方向向左平移4个单位长度，得到一条新的抛物线．
（1）求平移后的抛物线解析式；
（2）由抛物线对称轴知识我们已经知道：直线x=m，即为过点（m，0）平行于y轴的直线，类似地，直线y=m，即为过点（0，m）平行于x轴的直线、请结合图象回答：当直线y=m与这两条抛物线有且只有四个交点，实数m的取值范围；
（3）若将已知的抛物线解析式改为y=x2+bx+c（b＜0），并将此抛物线沿x轴向左平移-b个单位长度，试回答（2）中的问题．精英家教网
（2012•盐城模拟）如图a，在平面直角坐标系中，A（0，6），B（4，0）

（1）按要求画图：在图a中，以原点O为位似中心，按比例尺1：2，将△AOB缩小，得到△DOC，使△AOB与△DOC在原点O的两侧；并写出点A的对应点D的坐标为
（0，-3）
（0，-3）
，点B的对应点C的坐标为
（-2，0）
（-2，0）
；
（2）已知某抛物线经过B、C、D三点，求该抛物线的函数关系式，并画出大致图象；
（3）连接DB，若点P在CB上，从点C向点B以每秒1个单位运动，点Q在BD上，从点B向点D以每秒1个单位运动，若P、Q两点同时分别从点C、点B点出发，经过t秒，当t为何值时，△BPQ是等腰三角形？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网