题目内容
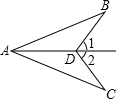 如图,已知∠1=∠2,在下列条件:①∠B=∠C;②∠BAD=∠CAD;③BD=CD;④AB=AC中,只补充一个就一定可以判断△ABD≌△ACD的条件是
如图,已知∠1=∠2,在下列条件:①∠B=∠C;②∠BAD=∠CAD;③BD=CD;④AB=AC中,只补充一个就一定可以判断△ABD≌△ACD的条件是
- A.①②③④
- B.①②③
- C.②③④
- D.①②④
B
分析:由题意可得,∠ADB=∠ADC,再加入①②利用AAS、ASA可证明△ABD≌△ACD,若加入③,利用AAS可证明△ABD≌△ACD,当加入④,没有SSA定理,可进行选择即可.
解答:∵∠1=∠2,
∴∠ADB=∠ADC,
∵∠B=∠C,
∴△ABD≌△ACD,故①正确;
∵∠BAD=∠CAD,
∴△ABD≌△ACD,故②正确;
∵BD=CD,
∴△ABD≌△ACD,故③正确.
∴故选B.
点评:本题考查了全等三角形的判定,判定三角形全等的方法:SSS、SAS、ASA、AAS,判断直角三角形全等的方法:“HL”.
分析:由题意可得,∠ADB=∠ADC,再加入①②利用AAS、ASA可证明△ABD≌△ACD,若加入③,利用AAS可证明△ABD≌△ACD,当加入④,没有SSA定理,可进行选择即可.
解答:∵∠1=∠2,
∴∠ADB=∠ADC,
∵∠B=∠C,
∴△ABD≌△ACD,故①正确;
∵∠BAD=∠CAD,
∴△ABD≌△ACD,故②正确;
∵BD=CD,
∴△ABD≌△ACD,故③正确.
∴故选B.
点评:本题考查了全等三角形的判定,判定三角形全等的方法:SSS、SAS、ASA、AAS,判断直角三角形全等的方法:“HL”.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
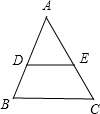 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =2,∠ADC=30°
=2,∠ADC=30°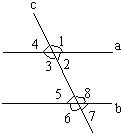 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
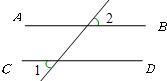 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=