��Ŀ����
����Ŀ����ͼ��������![]() �У���
�У���![]() Ϊֱ������Բ��
Ϊֱ������Բ��![]() .����������
.����������![]() ��
��![]() ���ֱ�ӵ�
���ֱ�ӵ�![]() ����
����![]() ͬʱ��������
ͬʱ��������![]() ���߶�
���߶�![]() ��
��![]() /����ٶ����
/����ٶ����![]() �˶�����
�˶�����![]() ������
������![]() ��
��![]() /����ٶ����
/����ٶ����![]() �˶�.����
�˶�.����![]() ����
����![]() ��ʱ��
��ʱ��![]() ��
��![]() ͬʱֹͣ�˶�,���
ͬʱֹͣ�˶�,���![]() �˶�ʱ��Ϊ
�˶�ʱ��Ϊ![]() .
.

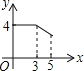
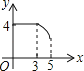
��1����![]() Ϊ��ֵʱ���߶�
Ϊ��ֵʱ���߶�![]() ��
��![]() ƽ��?
ƽ��?
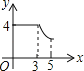
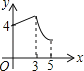
��2����![]() ����
����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ���Բ���У�
���Բ���У�
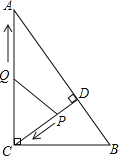
��3����ͼ2����ͼ�η���ֱ������ϵ�У���![]() ʱ����
ʱ����![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��˫����
��˫����![]() ������
������![]() ���������
���������![]() ���ڵ�
���ڵ�![]() �����˫���ߵĺ�����ϵʽ����ֱ��д��
�����˫���ߵĺ�����ϵʽ����ֱ��д��![]() ��ֵ.
��ֵ.
���𰸡���1����t=![]() ����2����t=
����2����t=![]() ����3����y=��
����3����y=��![]() ��
��![]() .
.
��������
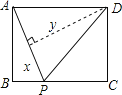
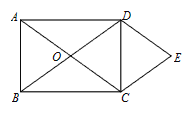
�����������1������ʱ��Ϊt����BE=t��CF=4��2t������BE=CF���t��ֵ����2������ʱ��Ϊt����F����FK��BC����AB��K����BE=t��CF=4��2t��EK=3t��4��EF=4��t������Rt��EKF�Ĺ��ɶ������t��ֵ���ó��𰸣���3������������ó�![]() ��������APE�ס�CPE�ó�
��������APE�ס�CPE�ó�![]() ���Ӷ�˵����P��λ����t����ֵ�أ�����AC�ij������CP�ij��ȣ��Ӷ��ó���P�����꣬���ô���ϵ���������������ʽ���ó���H�����꣬�Ӷ��ó���.
���Ӷ�˵����P��λ����t����ֵ�أ�����AC�ij������CP�ij��ȣ��Ӷ��ó���P�����꣬���ô���ϵ���������������ʽ���ó���H�����꣬�Ӷ��ó���.
�����������1������E��F������t��ʱ��EF��BC��
��ʱBE=t��CF=4��2t��BE=CF����t=4��2t����![]()
��2������E��F������t��ʱ��EF���Բ���У���F����FK��BC����AB��K.
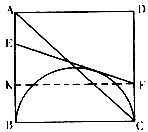
��BE=t��CF=4��2t��EK=EB��KB=EB��FC=t����4��2t��=3t��4 EF=BE+CF�����߳���ȣ�=4��t
��Rt��EKF��EF2=EK2+KF2=��4��t��2=��3t��4��2+22 ���:![]() ��
��![]() ����ȥ��
����ȥ��
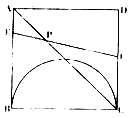
��3������1��t��2ʱ����ͼ����![]()
��AB��DC�����APE�ס�CPE ��![]() ����P��λ����t����ֵ��.
����P��λ����t����ֵ��.
��P��λ�ò��ᷢ���仯��AP��PC��ֵΪ![]() ����
����![]() ����AP��PC=1:2�ɵ�CP=
����AP��PC=1:2�ɵ�CP=![]()
��P��![]() ����˫���߽���ʽΪ
����˫���߽���ʽΪ![]() ����P��
����P��![]() �� �����
�� �����![]() ����
����![]()
��H��![]() �� ��
�� ��![]()