题目内容
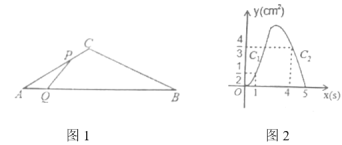
【题目】如图1,在![]() 中,
中, ![]() ,边
,边![]() 的长为
的长为![]() 边
边![]() 的长为
的长为![]() ,在此三角形内有一个矩形
,在此三角形内有一个矩形![]() ;点
;点![]() 分别在
分别在![]() 上,设
上,设![]() 的长为
的长为![]() ,矩形
,矩形![]() 的面积为
的面积为![]() (单位:
(单位: ![]() )
)
(1)当![]() 等于30时,求
等于30时,求![]() 与
与![]() 的函数关系式:(不要求写出自变量
的函数关系式:(不要求写出自变量![]() 的取值范围)
的取值范围)
(2)在(1)的条件下,矩形![]() 的面积能否为
的面积能否为![]() ?请说明理由?
?请说明理由?
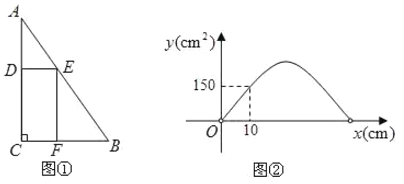
(3)若![]() 与
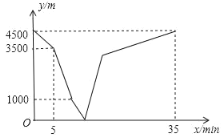
与![]() 的函数图象如图2所示,求此时
的函数图象如图2所示,求此时![]() 的值
的值
【答案】(1)![]() ;(2)不能为180,见详解;(3)h=40
;(2)不能为180,见详解;(3)h=40
【解析】
(1)根据AC的长,可用AD表示出CD,根据∠A的正切值,可用AD表示出DE,由此可得出关于y,x的函数关系式.
(2)将y=180代入(1)的函数式中,如果得出的方程有解,就说明矩形的面积能够成为180cm2,反之则不能.
(3)根据(1)的解题思路不难得出含h的关于x,y的函数关系式,然后将图象中的(10,150)的坐标代入抛物线的解析式中,即可求出h的值.
解:(1)∵AC=30,AD=x,
∴CD=30-x.
∵四边形CFED为矩形,
∴DE∥BC.
∴![]() ,即
,即![]() .
.
∴DE=![]() ,
,
∴y=![]() (30-x).
(30-x).
即y=![]() +20x.
+20x.
(2)∵ =150,
=150,
∴y的最大值为150.
∵150<180,
∴矩形CFED的面积不能为180cm2.
(3)由图象可知,当x=10时,y=150.
当x=10时,CD=h-10,DE=![]() ,
,
∴![]() (h-10)=150,
(h-10)=150,
解得h=40.
经检验h=40是方程的解.
∴h=40.

【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第![]() 天(
天(![]() 为整数)的售价、销量及储存和损耗费用的相关信息如表所示.
为整数)的售价、销量及储存和损耗费用的相关信息如表所示.
时间 |
|
|
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 |
销量(斤) |
|
|
储存和损耗费用(元) |
|
|
已知该种水果的进价为4.1元/斤,设销售该水果第![]() (天)的利润为
(天)的利润为![]() (元),求
(元),求![]() 与
与![]() (
(![]() )之间的函数解析式,并求出第几天时销售利润最大.
)之间的函数解析式,并求出第几天时销售利润最大.