题目内容
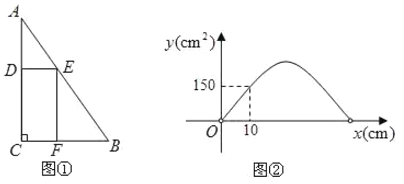
【题目】如图1中, ![]() ,点
,点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿折线
的速度沿折线![]() 运动,点
运动,点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 运动,
运动,![]() 两点同时出发,当某一点运动到点
两点同时出发,当某一点运动到点![]() 时,两点同时停止运动.设运动时间为
时,两点同时停止运动.设运动时间为![]() ,
,![]() 的面积为
的面积为![]() ),
),![]() 关于
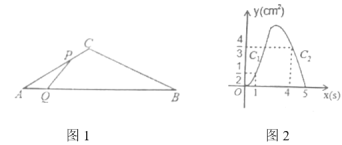
关于![]() 的函数图象由
的函数图象由![]() 两段组成,如图2所示,有下列结论:①
两段组成,如图2所示,有下列结论:①![]() ;②
;②![]() :③图象
:③图象![]() 段的函数表达式为
段的函数表达式为![]() ;④
;④![]() 面积的最大值为8,其中正确的个数有( )个
面积的最大值为8,其中正确的个数有( )个
A.1个B.2个C.3个D.4个
【答案】A
【解析】
①根据题意列出y=![]() APAQsinA,即可解答
APAQsinA,即可解答
②根据图像可知PQ同时到达B,则AB=5,AC+CB=10,再代入即可
③把sinB=![]() ,代入解析式即可
,代入解析式即可
④根据题意可知当x=﹣![]() 时,y最大=
时,y最大=![]()
解:①当点P在AC上运动时,y=![]() APAQsinA=
APAQsinA=![]() ×2xvx=vx2,
×2xvx=vx2,
当x=1,y=![]() 时,得v=1,
时,得v=1,
故此选项正确;
②由图象可知,PQ同时到达B,则AB=5,AC+CB=10,
当P在BC上时y=![]() x(10﹣2x)sinB,
x(10﹣2x)sinB,
当x=4,y=![]() 时,代入解得sinB=
时,代入解得sinB=![]() ,
,
故此选项正确;
③∵sinB=![]() ,
,
∴当P在BC上时y=![]() x(10﹣2x)×
x(10﹣2x)×![]() =﹣
=﹣![]() x2+
x2+![]() x,
x,
∴图象C2段的函数表达式为y=﹣![]() x2+
x2+![]() x,
x,
故此选项不正确;
④∵y=﹣![]() x2+
x2+![]() x,
x,
∴当x=﹣![]() 时,y最大=
时,y最大=![]() ,
,
故此选项不正确;
故选:A.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数,反比例函数或二次函数中的一种)
x(亩) | 20 | 25 | 30 | 35 |
y(元) | 1800 | 1700 | 1600 | 1500 |
(1)请求出种植樱桃的面积超过15亩时每亩获得利润y与x的函数关系式;
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过50亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.