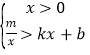��Ŀ����
����Ŀ���Ķ����ϣ�
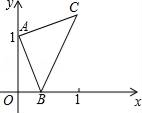
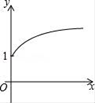
����֪����һ��ֱ�߾�������ֱ�������ε�ֱ�Ƕ��㣬��������������ֱ����ֱ�������ߣ����ɵ�����ֱģ�͡���ͼ�٣���![]() �У�
��![]() ��
��![]() ���ֱ��
���ֱ��![]() ��
��![]() ����
����![]() ֱ�������ߣ�����ֱ�Ϊ
ֱ�������ߣ�����ֱ�Ϊ![]() ��
��![]() �����Ǻ������ֽ��ۣ�
�����Ǻ������ֽ��ۣ�![]() ��
��

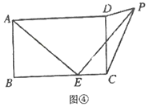
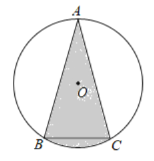
��1��̽�����⣺���![]() �������������䣬��ͼ�ڣ��ɵõ����ۣ�
�������������䣬��ͼ�ڣ��ɵõ����ۣ�![]() ������˵�����ɣ�
������˵�����ɣ�
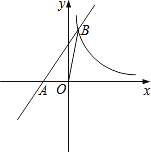
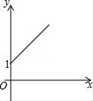
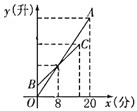
��2��ѧ�����ã���ͼ�ۣ���ƽ��ֱ������ϵ�У�ֱ��![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ������ֱ�н�Ϊ
������ֱ�н�Ϊ![]() ����
����![]() ���������ֱ��
���������ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
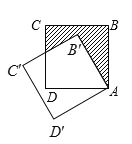
��3����չӦ�ã���ͼ�ܣ��ھ���![]() �У�
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() �����������㣬����
�����������㣬����![]() �����߶�
�����߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ����
����![]() ���ڵ�
���ڵ�![]() ��������
��������![]() �ھ���
�ھ���![]() �ⲿʱ������
�ⲿʱ������![]() ��
��![]() ����
����![]() Ϊֱ��������ʱ������̽����ֱ��д��
Ϊֱ��������ʱ������̽����ֱ��д��![]() �ij���
�ij���
���𰸡���1�����ɼ���������2��![]() ����3��
����3��![]() ��Ϊ3��
��Ϊ3��![]() ��
��
��������
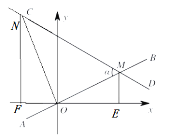
��1������ͬ�ǵ������ȵõ�![]() ��Ȼ������AA�����ж����������ƣ�
��Ȼ������AA�����ж����������ƣ�
��2������![]() ��
��![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ���ֱ��
���ֱ��![]() ��
��![]() ��
��![]() �ᣬ
�ᣬ![]() �ᣬ�ɣ�1����
�ᣬ�ɣ�1����![]() ���Ӷ��õ�
���Ӷ��õ�![]() ��Ȼ�������������ε����ʺ�������Ǻ������
��Ȼ�������������ε����ʺ�������Ǻ������![]() ��
��![]() ���Ӷ�ȷ��N�����꣬Ȼ�����ô���ϵ������������ʽ��
���Ӷ�ȷ��N�����꣬Ȼ�����ô���ϵ������������ʽ��
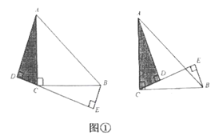
��3���������������ۣ�����ͼ1�У�����PDC=90��ʱ������ͼ2�У�����DPC=90��ʱ����PF��BC��F��PH��CD��H����BE=x���ֱ���⼴�ɣ�
�⣺��1����![]() ����
����![]()
�֡�![]()
��![]()
��![]()
��![]() ��
��
��![]()
��2����ͼ������![]() ��
��![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ��
��
�ֱ��![]() ��
��![]() ��
��![]() �ᣬ
�ᣬ![]() ��
��
�ɣ�1����![]() ��
��![]()
��![]() ����
����![]() ��
��![]() ��
��![]()
��![]() ��
��![]()
��ã�![]() ��
��![]() ��
��![]()
��ֱ��![]() ����ʽΪ
����ʽΪ![]() ������
������![]() ��
��![]()
��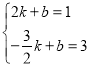 �����
�����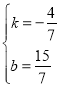 ��
��
��ֱ��![]() ����ʽΪ
����ʽΪ![]()
��3���⣺����ͼ1�У�����PDC=90��ʱ��
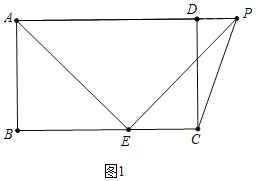
�ߡ�ADC=90����
���ADC+��PDC=180����
��A��D��P���ߣ�
��EA=EP����AEP=90����
���EAP=45�����ߡ�BAD=90����
���BAE=45�����ߡ�B=90��
���BAE=��BEA=45����
��BE=AB=3��
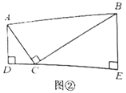
����ͼ2�У�����DPC=90��ʱ����PF��BC��F��PH��CD��H����BE=x��
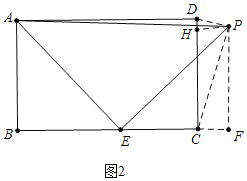
�ߡ�AEB+��PEF=90������AEB+��BAE=90����
���BAE=��PEF��
�ڡ�ABE�͡�EFP�У�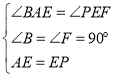
���ABE�ա�EFP��
��EF=AB=3��PF=HC=BE=x��
��CF=3-��5-x��=x-2��
�ߡ�DPH+��CPH=90������CPH+��PCH=90����
���DPH=��PCH���ߡ�DHP=��PHC��
���PHD�ס�CHP��
��PH2=DHCH��
�ࣨx-2��2=x��3-x����
��x=![]() ��
��![]() ����������
����������
��BE=![]() ��
��
��������������PDC��ֱ��������ʱ��BE��ֵΪ3��![]() ��
��