题目内容
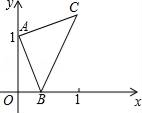
【题目】如右图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( )
A.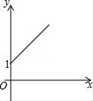 B.
B.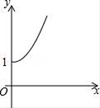
C.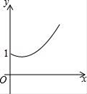 D.
D.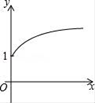
【答案】A
【解析】
先做出合适的辅助线,再证明△ADC和△AOB的关系,即可建立y与x的函数关系,从而确定函数图像.
解:由题意可得:OB=x,OA=1,∠AOB=90°,∠BAC=90°,AB=AC,点C的纵坐标是y,
作AD∥x轴,作CD⊥AD于点D,如图所示:
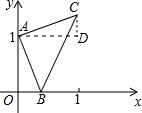
∴∠DAO+∠AOD=180°,
∴∠DAO=90°,
∴∠OAB+∠BAD=∠BAD+∠DAC=90°,
∴∠OAB=∠DAC,
在△OAB和△DAC中,
∠AOB=∠ADC,∠OAB=∠DAC,AB=AC
∴△OAB≌△DAC(AAS),
∴OB=CD,
∴CD=x,
∵点C到x轴的距离为y,点D到x轴的距离等于点A到x的距离1,
∴y=x+1(x>0).
故选A.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目