题目内容
(2013•天桥区一模)完成下列各题:
(1)如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD. 求证:BC=AD.
(2)如图,在△ABC中,∠A=30°,∠B=45°,AC=2
,求AB的长.

(1)如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD. 求证:BC=AD.
(2)如图,在△ABC中,∠A=30°,∠B=45°,AC=2
| 3 |

分析:(1)根据AC⊥BC,BD⊥AD,得出△ABC与△BAD是直角三角形,再根据AC=BD,AB=BA,得出Rt△ABC≌Rt△BAD,即可证出BC=AD,
(2)过C作CD⊥AB于D,求出∠BCD=∠B,推出BD=CD,根据含30度角的直角三角形求出CD,根据勾股定理求出AD,相加即可求出答案.
(2)过C作CD⊥AB于D,求出∠BCD=∠B,推出BD=CD,根据含30度角的直角三角形求出CD,根据勾股定理求出AD,相加即可求出答案.
解答: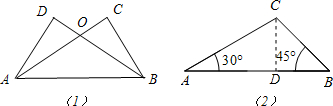 证明:(1)如图(1),∵AC⊥BC,BD⊥AD,
证明:(1)如图(1),∵AC⊥BC,BD⊥AD,
∴∠ADB=∠ACB=90°,
∴在Rt△ABC和Rt△BAD中,
,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD;
(2)如图(2),过C作CD⊥AB于D,
∴∠ADC=∠BDC=90°,
∵∠B=45°,
∴∠BCD=∠B=45°,
∴CD=BD,
∵∠A=30°,AC=2
,
∴CD=
,
∴BD=CD=
,
由勾股定理得:AD=
=3,
∴AB=AD+BD=3+
.
答:AB的长是3+
.
 证明:(1)如图(1),∵AC⊥BC,BD⊥AD,
证明:(1)如图(1),∵AC⊥BC,BD⊥AD,∴∠ADB=∠ACB=90°,
∴在Rt△ABC和Rt△BAD中,
|
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD;
(2)如图(2),过C作CD⊥AB于D,
∴∠ADC=∠BDC=90°,
∵∠B=45°,
∴∠BCD=∠B=45°,
∴CD=BD,
∵∠A=30°,AC=2
| 3 |
∴CD=
| 3 |
∴BD=CD=
| 3 |
由勾股定理得:AD=
| AC2-CD2 |
∴AB=AD+BD=3+
| 3 |
答:AB的长是3+
| 3 |
点评:本题考查了全等三角形的判定及性质,勾股定理,等腰三角形的性质和判定,含30度角的直角三角形性质等知识点的应用,关键是构造直角三角形,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
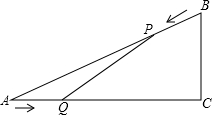 (2013•天桥区一模)如图,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA向点A匀速运动,同时点Q由A出发沿AC向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).
(2013•天桥区一模)如图,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA向点A匀速运动,同时点Q由A出发沿AC向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).