题目内容
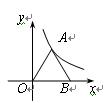
如图,将一块直角三角形纸板的直角顶点放在 处,两直角边分别与
处,两直角边分别与 轴平行,纸板的另两个顶点
轴平行,纸板的另两个顶点 恰好是直线
恰好是直线 与双曲线
与双曲线 的交点.
的交点.

(1)求 和
和 的值;
的值;
(2)设双曲线 在
在 之间的部分为
之间的部分为 ,让一把三角尺的直角顶点
,让一把三角尺的直角顶点 在
在 上
上
滑动,两直角边始终与坐标轴平行,且与线段 交于
交于 两点,请探究是否存在点
两点,请探究是否存在点 使得
使得 ,写出你的探究过程和结论.
,写出你的探究过程和结论.
 处,两直角边分别与
处,两直角边分别与 轴平行,纸板的另两个顶点
轴平行,纸板的另两个顶点 恰好是直线
恰好是直线 与双曲线
与双曲线 的交点.
的交点.
(1)求
 和
和 的值;
的值;(2)设双曲线
 在
在 之间的部分为
之间的部分为 ,让一把三角尺的直角顶点
,让一把三角尺的直角顶点 在
在 上
上滑动,两直角边始终与坐标轴平行,且与线段
 交于
交于 两点,请探究是否存在点
两点,请探究是否存在点 使得
使得 ,写出你的探究过程和结论.
,写出你的探究过程和结论.(1)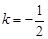 且
且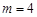 (2)不存在,证明见解析
(2)不存在,证明见解析
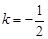 且
且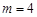 (2)不存在,证明见解析
(2)不存在,证明见解析解:(1)∵ 在双曲线
在双曲线 上,
上,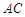 ∥
∥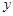 轴,
轴, ∥
∥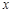 轴,
轴,
∴A,B的坐标分别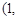
 ,
,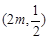 . ……………………(1分)
. ……………………(1分)
又点A,B在直线 上,∴
上,∴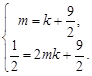 ……………………(2分)
……………………(2分)
解得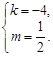 或
或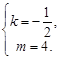 …………………(4分)
…………………(4分)
当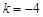 且
且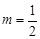 时,点A,B的坐标都是
时,点A,B的坐标都是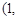
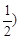 ,不合题意,应舍去;当
,不合题意,应舍去;当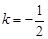
且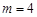 时,点A,B的坐标分别为
时,点A,B的坐标分别为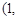
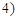 ,
,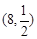 ,符合题意.
,符合题意.
∴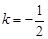 且
且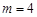 .………………………………………………………………(5分)
.………………………………………………………………(5分)
(2)假设存在点 使得
使得 .
.
∵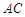 ∥
∥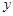 轴,
轴, ∥
∥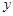 轴,∴
轴,∴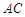 ∥
∥ ,
,
∴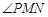
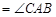 ,∴Rt
,∴Rt ∽Rt
∽Rt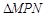 ,∴
,∴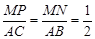 ,……………(7分)
,……………(7分)
设点P坐标为 (1<x<8=,则M点坐标为
(1<x<8=,则M点坐标为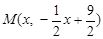 ,
,
∴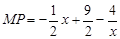 .又
.又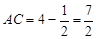 ,
,
∴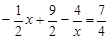 ,即
,即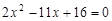 (※) ……………………(9分)
(※) ……………………(9分)
∵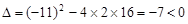 .∴方程(※)无实数根.
.∴方程(※)无实数根.
所以不存在点 使得
使得 . …………………(10分)
. …………………(10分)
(1)根据题意可设出A、B两点的坐标,把A、B两点的坐标代入直线y="kx+"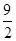 ,与双曲线y=
,与双曲线y= 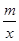 (m>0)可得到关于mk的方程组,求出m、k的值即可.
(m>0)可得到关于mk的方程组,求出m、k的值即可.
(2)本题考查的是一次函数及反比例函数图象上点的坐标特点,根据题意设出A、B两点的坐标,是解答此题的关键.
 在双曲线
在双曲线 上,
上,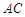 ∥
∥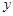 轴,
轴, ∥
∥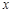 轴,
轴,∴A,B的坐标分别
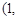
 ,
,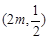 . ……………………(1分)
. ……………………(1分)又点A,B在直线
 上,∴
上,∴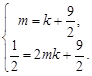 ……………………(2分)
……………………(2分)解得
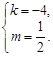 或
或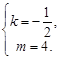 …………………(4分)
…………………(4分)当
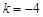 且
且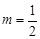 时,点A,B的坐标都是
时,点A,B的坐标都是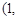
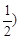 ,不合题意,应舍去;当
,不合题意,应舍去;当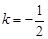
且
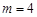 时,点A,B的坐标分别为
时,点A,B的坐标分别为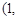
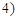 ,
,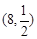 ,符合题意.
,符合题意.∴
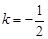 且
且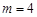 .………………………………………………………………(5分)
.………………………………………………………………(5分)(2)假设存在点
 使得
使得 .
.∵
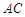 ∥
∥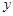 轴,
轴, ∥
∥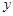 轴,∴
轴,∴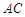 ∥
∥ ,
,∴
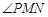
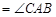 ,∴Rt
,∴Rt ∽Rt
∽Rt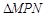 ,∴
,∴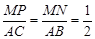 ,……………(7分)
,……………(7分)设点P坐标为
 (1<x<8=,则M点坐标为
(1<x<8=,则M点坐标为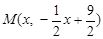 ,
,∴
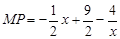 .又
.又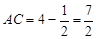 ,
,∴
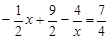 ,即
,即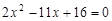 (※) ……………………(9分)
(※) ……………………(9分)∵
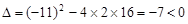 .∴方程(※)无实数根.
.∴方程(※)无实数根.所以不存在点
 使得
使得 . …………………(10分)
. …………………(10分)(1)根据题意可设出A、B两点的坐标,把A、B两点的坐标代入直线y="kx+"
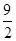 ,与双曲线y=
,与双曲线y= 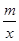 (m>0)可得到关于mk的方程组,求出m、k的值即可.
(m>0)可得到关于mk的方程组,求出m、k的值即可.(2)本题考查的是一次函数及反比例函数图象上点的坐标特点,根据题意设出A、B两点的坐标,是解答此题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
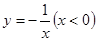 的图象大致是( )
的图象大致是( )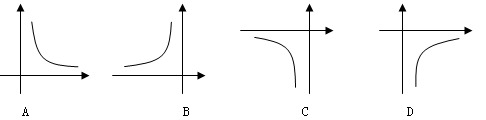
 与反比例函数
与反比例函数 的图象交于点
的图象交于点 则
则 的值是( ).
的值是( ). 或
或
 或
或
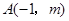 与
与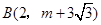 是反比例函数
是反比例函数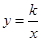 图象上的两个点.
图象上的两个点.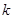 的值;
的值;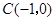 ,则在反比例函数
,则在反比例函数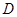 ,使得以
,使得以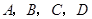 四点为顶点的四边形为梯形?若存在,求出点
四点为顶点的四边形为梯形?若存在,求出点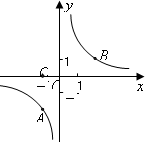
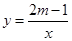 的图象如图所示,
的图象如图所示,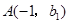 ,
,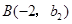 是该图象上的两点。
是该图象上的两点。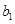 与
与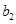 的大小;
的大小;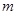 的取值范围。
的取值范围。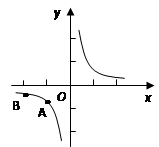
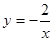 图象上有两点A(x1,y1)和 B(x2,y2),若y1<y2<0, 则x1与x2的关系是( )
图象上有两点A(x1,y1)和 B(x2,y2),若y1<y2<0, 则x1与x2的关系是( )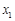 ,
,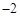 ),(
),(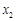 ,2),(
,2),(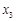 ,3)都在反比例函数
,3)都在反比例函数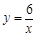 的图象上,则下列关系中正确的是
的图象上,则下列关系中正确的是 



 的图象经过点(-l,
的图象经过点(-l, ),则
),则