题目内容
【题目】A校和B校分别库存有电脑12台和6台,现决定支援给C校10台和D校8台.已知从A校调运一台电脑到C校和D校的运费分别为40元和10元;从B校调运一台电脑到C校和D校的运费分别为30元和20元. 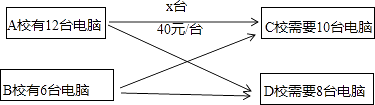
(1)设A校运往C校的电脑为x台,请仿照下图,求总运费W(元)关于x的函数关系式;
(2)求出总运费最低的调运方案,最低运费是多少?
【答案】
(1)解:∵从A校调往C校x台,
∴从A校调往D校(12﹣x)台,从B校调往C校(10﹣x)台,调往D校[6﹣(10﹣x)]=(x﹣4)台,
∴W=40x+10(12﹣x)+30(10﹣x)+20(x﹣4)=20x+340,
∵机器的台数只能是正整数,
∴12﹣x≥0且 10﹣x≥0 且 x﹣4≥0
解得:4≤x≤10,且x为正整数,
∴运费W关于x的函数关系式为:W=20x+340 (4≤x≤10)
(2)解:∵W=20x+340(4≤x≤10)是一次函数,
∴当x=4时,运费W最低,此时W=420,
即总运费最低的调运方案是:从A校调运4台电脑到C校,调运8台电脑到D校,从B校调运6台电脑到C校,最低费用是420元
【解析】(1)根据题意可以求得总运费W(元)关于x的函数关系式,注意x必须是非负整数;(2)根据(1)中的函数关系和一次函数的性质可以解答本题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目




