题目内容
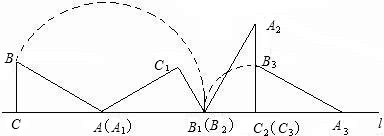
如图,在直角三角形△ABC中,∠C=90°,∠BAC=30°,BC=1cm.将△ABC沿直线L从左向右翻转3次,则点B经过的路程等于
- A.
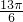 cm
cm - B.
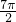 cm
cm - C.
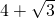 cm
cm - D.
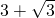 cm
cm
A
分析:翻转三次即是二段弧长,所以根据弧长公式可求.
解答:第一次旋转是以点A为圆心,AB为半径,旋转的角度是180-30=150度;
第二次是以点B为圆心,所以B路程没变;
第三次是以点C为圆心,半径是BC,旋转的度数是90;
所以根据弧长公式可得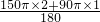 =
=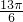 cm.
cm.
故选A.
点评:本题的关键是弄准二段弧长的半径及圆心角和圆心的位置.
分析:翻转三次即是二段弧长,所以根据弧长公式可求.
解答:第一次旋转是以点A为圆心,AB为半径,旋转的角度是180-30=150度;
第二次是以点B为圆心,所以B路程没变;
第三次是以点C为圆心,半径是BC,旋转的度数是90;
所以根据弧长公式可得
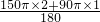 =
=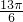 cm.
cm.故选A.
点评:本题的关键是弄准二段弧长的半径及圆心角和圆心的位置.

练习册系列答案
相关题目
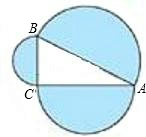 如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )
如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )| A、2π | B、3π | C、4π | D、6π |
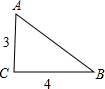
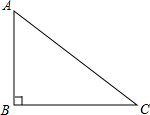 如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.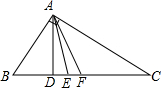 如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,
如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,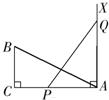 9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=
9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=