题目内容
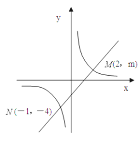
【题目】如图，一次函数y=k1x+b的图象与反比例函数
的图象交于M、N两点．
（1）求反比例函数和一次函数的解析式；
（2）根据图象写出使反比例函数的值大于一次函数的值的x的取值范围．
【答案】（1）
， y=2x﹣2;（2）x＜﹣1或0＜x＜2．
【解析】
（1）将点M（2，m），N（-1，-4）代入反比例函数y＝
中得：2m=（-1）×（-4）=k2，可求k1、m；再将点M（2，m），B（-1，-4）代入y=k1x+b中，列方程组求k1、b即可；
（2）反比例函数值大于一次函数值，即反比例函数的图象在一次函数的图象的上方时自变量的取值范围即可．
（1）∵反比例函数
图象过点（﹣1，﹣4），
∴k2=﹣1×（﹣4）=4，
∵反函数图象过点（2，m），
∴m=2，
由直线y=k1x+b过点M，N，得 
，
解得
，
∴反比例函数关系式为
，一次函数关系式为y=2x﹣2；
（2）从图象可以看出当x＜﹣1或0＜x＜2时，反比例函数的值大于一次函数的值，
故使反比例函数的值大于一次函数的值的x的取值范围为x＜﹣1或0＜x＜2．
练习册系列答案
相关题目
